Prédire à partir de la régression logistique

Principe

La régression logistique est un modèle de régression binomiale. Elle permet de mesurer l’association entre la survenue d’un évènement (variable expliquée qualitative) et les facteurs susceptibles de l’influencer (variables explicatives). En d’autres termes, il s’agit d’associer à un vecteur de variables aléatoires une variable aléatoire binomiale (2 modalités) génériquement notée .

Le modèle de régression logistique permet donc de prédire la probabilité qu’un événement arrive (valeur de 1) ou non (valeur de 0). Le résultat varie toujours entre 0 et 1. Lorsque la valeur prédite est supérieure à un seuil, l’événement est susceptible de se produire, alors que lorsque cette valeur est inférieure au même seuil, il ne l’est pas.

Représentation

Les fonctions les plus couramment utilisées pour relier la probabilité p aux variables explicatives sont la fonction logistique (on parle alors de modèle Logit) et la fonction de répartition de la loi normale standard (on parle alors de modèle Probit). Ces deux fonctions sont parfaitement symétriques et sigmoïdes, bornée par 0, et 1.

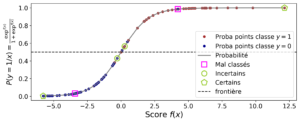
Probabilité de réalisation d’un évènement (p) en fonction des valeurs prises par une variable (X) variant de (0 à 1) selon la fonction logistique.

Formulation

Lorsque la fonction logistique est ajustée à des données observées, la forme de la courbe sigmoïde s’adapte à ces données, par l’estimation de paramètres. Dans le cas d’une seule variable explicative (X), l’équation de la courbe logistique est alors :