Explorer les données

Définitions

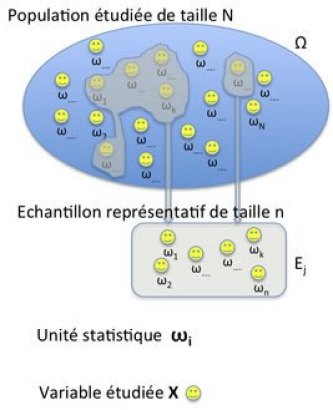
La statistique a pour objet de recueillir des observations portant sur des sujets présentant une certaine propriété et de traduire ces observations par des nombres qui permettent d’avoir des renseignements sur cette propriété.

On appelle population un ensemble d’éléments homogènes auxquels on s’intéresse. Par exemple, les étudiants d’une classe, les contribuables français, les ménages lillois . . .

Les éléments de la population sont appelés les individus ou unités statistiques.

Des observations concernant un thème particulier ont été effectuées sur ces individus. La série de ces observations forme ce que l’on appelle une variable statistique.

Lorsque le caractère étudié est exprimable directement par un nombre, l’énumération des nombres exprimant la valeur de ce caractère pour chaque membre de la population étudiée est une série statistique quantitative.

Analyse univariée

la tendance centrale

-Le mode, désigné par Mo est la valeur de la variable statistique la plus fréquente.

-La médiane, désignée par Me, est la valeur de la variable telle qu’il y ait autant d’observations, en dessous d’elle qu’au-dessus ou, ce qui revient au même, la valeur correspondant à 50% des observations.

-La moyenne de la série se note m. Elle exprime la grandeur qu’aurait chacun des membres de l’ensemble s’ils étaient tous identiques sans changer la dimension globale de l’ensemble.

la dispersion

-La différence entre la plus grande valeur et la plus petite valeur du caractère effectivement obtenue est l’étendue (noté e).

-Le nombre de membres de la population étudiée est l’effectif total.

-La fréquence d’une valeur (ou d’une classe) est le rapport de l’effectif de cette valeur (ou de cette classe) par l’effectif total.

–la variance est un indice de dispersion pour les variables numériques. Elle donne une indication de l’étendue de la variation des valeurs autour de la moyenne pour une variable donnée.

–l’écart-type est a racine carrée de la variance. Elle est très utile pour comparer 2 populations.

–le minimum et le maximum permettent de connaître la dispersion d’une variable.

l’intervalle de confiance

Elle permet de mesurer la marge d’erreur entre les données d’un échantillon et celles de la population totale. L’indice de confiance permet de calculer le risque d’erreur entre l’échantillon et la population.

les statistiques descriptives

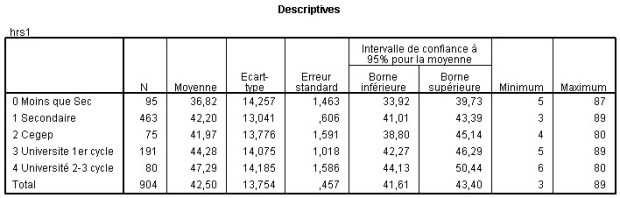
Le but de la statistique descriptive est de structurer et de représenter l’information contenue dans les données pour mieux les analyser.

Exemple de tableau de statistique descriptive

Représentation graphique

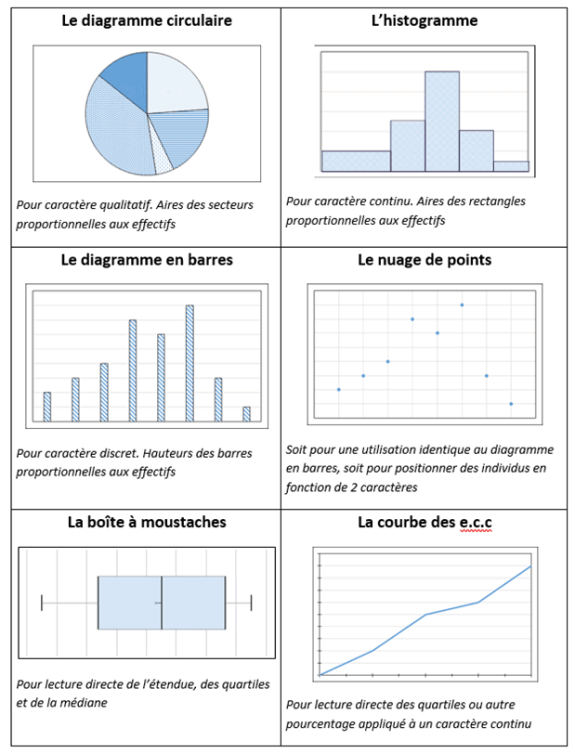
La représentation graphique est une synthèse de l’information qui fait apparaître la forme globale de la distribution des données. Le choix du type de graphe dépend de la nature des variables. Un graphique comprend trois parties:

• Un Titre
• Des coordonnées
• Des échelles (souvent arithmétiques) avec la valeur 0 au point de rencontre des 2 axes

Analyse bivariéee (relation entre les variables)

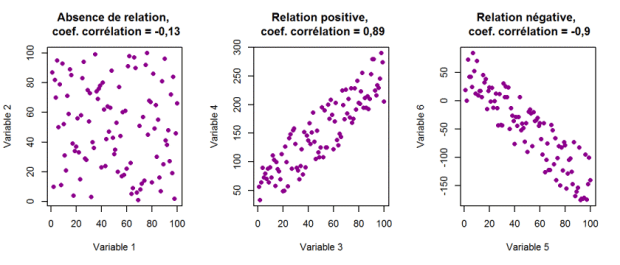
Pour savoir s’il existe une relation entre deux caractères, on établit un diagramme de corrélation, c’est à dire un diagramme croisant les modalités de X et de Y. Chaque élément i est représenté par le point de coordonnées (Xi,Yi). L’ensemble des points forme un nuage de points dont la forme permet de caractériser la relation à l’aide de trois critères : l’intensité de la relation, la forme de la relation et le sens de la relation.

Deux événements (appelons les X et Y) sont corrélés si l’on observe une dépendance, une relation entre les deux. Par exemple, le nombre de cheveux d’un homme a tendance à diminuer avec l’âge : âge et nombre de cheveux sont donc corrélés.