Découvrir des similarités à partir du partitionnement (Clustering)

Découvrir des similarités à partir du clustering

Le but du clustering est de créer des groupes (catégories) de points de données de telle sorte que les points dans différents clusters sont différents tandis que les points au sein d’un cluster sont similaires.

Le clustering vise donc à diviser un ensemble de données en différents « paquets » homogènes, en ce sens que les données de chaque sous-ensemble partagent des caractéristiques communes, qui correspondent le plus souvent à des critères de proximité (similarité informatique) que l’on définit en introduisant des mesures et classes de distance entre objets.

Méthodes

Le partitionnement de données est une méthode de classification non supervisée (différente de la classification supervisée où les données d’apprentissage sont déjà étiquetées), et donc parfois dénommée comme telle.

Il existe de 3 grandes familles de méthodes pour mesurer la similarité entre deux individus :

  • les méthodes centroïdes avec les algorithmes des k-moyennes ou k-médoïdes ;
  • les méthodes de regroupement hiérarchique ;
  • les méthodes à densité

Méthode centroïde

Étant donnés des points et un entier k, le problème est de diviser les points en k groupes, souvent appelés clusters, de façon à minimiser une certaine fonction. On considère la distance d’un point à la moyenne des points de son cluster ; la fonction à minimiser est la somme des carrés de ces distances.

Le principe de l’algorithme est de création d’une partition initiale de K classes, puis itération d’un processus qui optimise le partitionnement en déplaçant les objets d’une classe à l’autre.

Dans le clustering K-means, la façon dont ces groupes sont définis consiste à créer un centre de gravité (centroïde) pour chaque groupe. Les centroïdes sont comme le cœur du cluster, ils «capturent» les points les plus proches d’eux et les ajoutent au cluster.

Les étapes sont les suivantes:

  • Fixer le nombre de classes a priori K
  • Initialiser aléatoirement les centres (K individus tirés au hasard comme représentants des classes)
  • Affecter chaque observation à la classe qui minimise la distance entre le centre et l’observation (centre le plus proche)
  • Recalculer les nouveaux vecteurs centres (la moyenne)
  • Itérer l’opération jusqu’à la stabilité
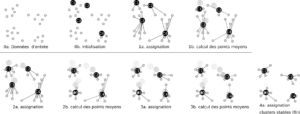
Toutefois, le clustering à partir du  partitionnement présente quelques difficultés:
  • nécessite de spécifier le nombre de classes à l’avance
  • utilisable seulement quand la notion de moyenne existe (donc pas sur des données nominales)
  • l’algorithme est sensible au bruit et aux anomalies
  • l’algorithme est sensibilité aux conditions d’initialisation (on n’obtiendra pas forcément les mêmes classes avec des partitionnements initiaux différents)
Passer au chapitre suivant