Analyse des graphes

Propriétés des grands réseaux

Il existe un ensemble de propriétés mathématiques qui ont été relevé lors de l’étude des grands graphes terrain (Strogartz, 2001). En effet, tous les grands réseaux sociaux possèdent tous :

• Le principe de l’attachement préférentiel (preferential attachment – Barabasi, 1999) constate que « les riches deviennent plus riches », c’est-à-dire que dans beaucoup de cas les nœuds les plus connectés gagnent aussi plus facilement des nouvelles L’attachement préférentiel se caractérise par une hétérogénéité des degrés et un faible degré moyen.
• L’effet du « petit monde » (Milgram, 1967) montre que dans une société de masse, pratiquement tous les individus sont reliés les uns aux autres dans un vaste réseau, et que la distance moyenne entre deux individus quelconques devrait être d’environ 5 intermédiaires. L’effet du « petit monde » se caractérise donc par des chemins courts entre les sommets.
• L’effet d’agglomération (clustering) correspond au principe suivant : mes amis ont une forte probabilité d’être eux-mêmes amis. L’effet d’agglomération (clustering) se caractérise par par un réseaux avec une densité globale faible et une densité locale forte
• Le principe de l’équivalence structurale (White, 2008) s’illustre lorsque deux entités sont structurellement équivalentes au sein d’un réseau si elles y occupent la même place, ou la même position, c’est-à-dire si elles ont les mêmes relations (ou des relations relativement similaires) avec un ensemble d’acteurs données . La notion d’équivalence structurelle permet donc de retrouver la notion classique de rôle (ou de position) mais d’un point de vue strictement structurel, par une analyse de réseau, sans faire d’hypothèse sur les contenus de ces rôles.
• La force des liens faibles est un concept popularisé par Granovetter (1973). Pour lui, ce sont leurs liens faibles qui procurent aux individus des informations qui ne sont pas disponibles dans leur cercle restreint : « Les individus avec qui ont est faiblement lié ont plus de chances d’évoluer dans des cercles différents et ont donc accès à des informations différentes de celles que l’on reçoit. »
• Les trous structuraux (Burt, 1992) correspond à une propriété d’intermédiaire au sein d’un réseau. Par exemple, une entreprise A, en relation avec deux autres B et C, sans que ces dernières ne le soient entre elles, dispose d’un avantage qu’elle est tentée d’exploiter à son profit. Cette position d’intermédiaire procure une autonomie à l’entreprise A. Les marchés sont donc  organisés par le fait que des acteurs cherchent à accroître leur «autonomie structurale».

Graphe biparti

En théorie des graphes, un graphe est dit biparti si son ensemble de sommets peut être divisé en deux sous-ensembles disjoints U et V tels que chaque arête ait une extrémité dans U et l’autre dans V.

Un graphe biparti permet notamment de représenter une relation binaire.

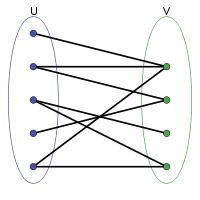
L’une des méthodes les plus courantes pour analyser ces graphes est de les transformer en deux graphes distincts de co-occurrence : le graphe acteur – événement est donc transformé en un graphe acteurs – acteurs (un lien entre deux acteurs indique qu’ils étaient tous deux présents à un même événement) et un graphe événement – événement (un lien entre deux événements indique que le même acteur a assisté aux deux). La figure 1 montre comment s’effectue ces transformations.

Dynamique d’un réseau

Définition

Un graphe dynamique est un réseau dans lequel des noeuds et des liens apparaissent et disparaissent au cours du temps. En effet, la plupart des graphes de terrain sont dynamiques, c’est-à-dire que leur structure évolue au fil du temps par l’ajout et/ou le retrait de noeuds et/ou de liens, à des fréquences
plus ou moins grandes.

Analyse de la dynamique

Pour réduire la complexité de l’analyse de la dynamique:

1. il faut se limiter aux réseaux croissants, dans lesquels les liens et les noeuds apparaissent, mais ne disparaissent jamais.
2. commencer par l’analyse d’un instantané
3. choisir la bonne granularité: si granularité trop petite, alors on perd le côté gros grains; si granularité trop grande, alors on perd la dynamique.

Voilà quelques métriques:

• évolution d’apparition de nouveaux noeuds
• évolution d’apparition de nouveaux liens
• évolution de disparition de noeuds
• évolution de disparition de liens
• noeuds ou liens qui réapparaissent après avoir disparu
• durée de vie moyenne des noeuds et des liens
• nombre d’apparition/disparition moyen

Pour aller plus loin sur la dynamique des réseaux

• Visualisez dynamiquement le crawl du Googlebot avec Gephi
• Gephi réseaux dynamiques. Clément Levallois
• A Tutorial – on dynamic networks with Gephi