Citation
L'auteur
Soufian SALIM
(soufian.salim@bee4win.com) - Bee4win
Copyright
Déclaration d'intérêts
Financements
Aperçu
Contenu
Introduction
Lors d’un appel d’offre, les entreprises sont mises en concurrence pour obtenir un marché public et seul le gagnant peut récupérer les frais de soumission. Pour une entreprise, la décision de soumettre une offre (« go ») ou non (« no go ») dépend de plusieurs facteurs : faisabilité technique, faisabilité commerciale, compétitivité, etc.
Répondre à un appel d’offre est un processus coûteux, et savoir prendre la bonne décision nécessite d’être bien informé. L’objectif du challenge « Prévoir l’attribution d’un marché public en fonction de la réputation de l’entreprise » est de fournir des prévisions pouvant être utiles à cette prise de décision. Les trois questions qui sont posées sont :
- Combien d’offres seront reçues ?
- Quel sera le montant de l’offre retenue ?
- Le marché peut-il être remporté par une petite ou moyenne entreprise ?
Dans cet article, nous rapportons les résultats d’expériences d’apprentissage statistique effectuées dans l’objectif de répondre à ces questions.
Données
Source
Le jeu de données utilisé pour ce challenge est issu de la commande publique de l’Union Européenne. Les avis de marchés qu’il contient couvrent l’ensemble de l’espace économique européen pour une période allant de 2009 à 2016. Toutes les données sont disponibles en ligne sur le Tenders Electronic Daily (TED).
Composition des données
Le jeu d’entraînement compte plus de deux millions de lignes, le jeu de test en comprenant environ un million. Chaque instance comporte dix-huit variables, telles que l’année de publication, le code CPV ou le type de procédure. En plus de ces informations, les trois valeurs à prédire sont :
- si le contrat est susceptible d’être gagné par des petites ou moyennes entreprises,
- le nombre d’offres reçues
- la valeur totale du marché, ou, si cette donnée est manquante, la proposition la plus basse.
Limites
La principale limitation à l’exploitabilité de ces données est posée par le fait que de nombreuses instances correspondent à différents lots d’un même marché. Si les données utilisées comme traits d’apprentissage correspondent au marché tandis que l’information à prédire correspond à une attribution, comme c’est le cas pour le nombre d’offres ou le montant du marché, alors il est possible – et même fréquent – que ces données comportent plusieurs fois les mêmes ensembles de variables indépendantes, mais des valeurs à prédire différentes. Cela signifie, de facto, que les « variables dépendantes » sont, en réalité, indépendantes, et donc impossibles à prédire.
En effet, sur les deux millions d’éléments du jeu d’entraînement, il n’existe que 700 000 combinaisons uniques de variables indépendantes. C’est-à-dire que pour chaque élément, il y a en moyenne trois montants et trois nombres d’offres différents.
Cette limitation est aggravée, dans le cas de la prédiction du montant, par le fait que la variable à prédire peut correspondre soit au montant réel, soit à l’offre la plus basse. Il n’est pas possible d’affirmer que ces deux valeurs correspondent à la même réalité empirique, et les modèles qui permettent de les prédire devraient probablement être entraînés séparément, ce qu’il n’est pas possible de faire avec les données disponibles.
Si ces limites ne rendent pas impossible l’expérimentation sur ces données avec des techniques d’apprentissage statistique, elles limitent conséquemment la fiabilité des résultats obtenus.
Méthodologie
Tâches
Le challenge se décompose en trois tâches. Deux d’entre elles sont des tâches de régression : la prédiction du nombre d’offres, et la prédiction de la valeur du marché. La troisième est une tâche de classification binaire : savoir si oui ou non l’offre peut être remportée par une PME.
Évaluation
Les expériences effectuées emploient un sous-ensemble de 100 000 instances extraites aléatoirement du jeu de données. Les résultats sont calculés par validation croisée (Weiss, S. M., & Kulikowski, C. A., 1991) avec k=10. Ainsi, pour chaque tâche, chaque classifieur est entrainé dix fois sur un sous-ensemble de 90 000 instances et évalué sur les 10 000 restantes, de manière à ce que l’ensemble des données puisse être employé pour l’évaluation. Le score final est calculé sur l’ensemble des prédictions.
Métriques
Pour évaluer les résultats, nous utilisons différentes métriques selon qu’il s’agisse d’une tâche de classification ou de régression.
Pour la classification, nous employons les trois mesures classiques pour ce type de tâche : la précision, le rappel, et la F-mesure, qui est la moyenne harmonique de la précision et du rappel.
Pour évaluer les tâches de régression, nous employons le Mean Absolute Error (MAE), le Root-Mean-Square Error (RMSE) et le Root-Mean-Square Logarithmic Error (RMSE). Contrairement au MAE, le RMSE calcule l’erreur moyenne entre les carrés des résultats, ce qui augmente l’impact des larges erreurs sur le score (Chai, T., & Draxler, R. R., 2014). Le RMSLE se comporte de manière similaire, mais calcule les erreurs à partir des valeurs logarithmiques, ce qui réduit l’impact des valeurs élevés quand les résultats varient de manière très conséquente.
Les résultats obtenus sont comparés à la méthode aléatoire (pour toutes les tâches) et à la médiane (pour les tâches de régression).
Cadre expérimental
Prétraitements
Quatorze des variables indépendantes sont catégorielles. Pour pouvoir les employer dans notre algorithme, nous les convertissons en matrices binaires, chaque colonne de ces matrices correspondant à une catégorie possible pour cette instance. La variable CPV contenant un très grand nombre de catégories possibles, nous ne retenons que ses quatre premiers chiffres pour réduire son espace vectoriel et ainsi éviter, d’une part, que le label CPV prenne une importance disproportionnée dans le modèle, et, d’autre part, pour éviter que de trop grands vecteurs de traits augmentent significativement les temps de calcul.
Algorithmes
Dans le cadre de nos expérimentations, nous employons différents algorithmes. Les classifieurs utilisés sont les suivants :
- NaiveBayes: le modèle bayésien naïf est un modèle probabiliste basé sur le théorème de Bayes. Ces modèles sont simples et ignorent les dépendances statistiques des caractéristiques observées, cependant ils ont fait preuve d’efficacité dans un grand nombre de tâches (Zhang, H., 2004).
- RandomForest: une forêt d’arbres décisionnels est un modèle basé sur l’entraînement de multiples arbres de décision disposant de différents sous-ensembles du jeu de données, et choisissant une prédiction en fonction des différents résultats obtenus (Breiman, L., 2001).
- Support Vector Machines (SVM) : les SVM sont des algorithmes de classification linéaire ayant souvent obtenu d’excellents résultats dans un grand ensemble de tâches, encore aujourd’hui concurrents des réseaux de neurones pour les performances état-de-l’art dans de nombreux domaines (Cortes, C., & Vapnik, V., 1995).
- NeuralNet : les performances des réseaux de neurones profonds ont dramatiquement augmenté avec le développement des nouvelles générations de GPU. Dans nos expériences nous employons un réseau à trois couches denses, et employons le MSE comme métrique, une optimisation Adam (Kingma, D. P., & Ba, J., 2014) et ReLU comme fonction d’activation.
Pour les tâches de régression, nous effectuons nos expériences avec les algorithmes suivants :
- Stochastic Gradient Descent (SGD) : la descente de gradient stochastique est une méthode itérative cherchant à minimiser une fonction objective (Zhang, T., 2004).
- Lasso : il s’agit d’un modèle de régression linéaire. Le modèle applique une régularisation de L1, qui a l’avantage d’intégrer un sélection de traits (Tibshirani, R., 1996).
- Régularisation de Tikhonov (Ridge) : similaire à Lasso, la régularisation de Tikhonov s’en distingue notamment en effectuant une régularisation de L2 (Phillips, D. L., 1962).
Expériences
Prédire si une PME peut remporter le marché
Pour cette première tâche, nous employons les algorithmes de classification décrits à la section précédente. Étant donné que le label n’est pas disponible pour toutes les lignes du jeu de données, nous ne conservons que celles pour lesquelles la valeur « Oui » ou « Non » est présente et considérons la tâche comme une tâche de classification à deux classes. Le résultat des expériences est rapporté au Tableau 1.
| P | R | F1 | |
| Aléatoire | 49,97 | 49,97 | 49,97 |
| NaiveBayes | 63,30 | 63,38 | 63,11 |
| RandomForest | 64,27 | 64,05 | 64,09 |
| SVM | 64,12 | 63,88 | 63,92 |
| NeuralNet | 65,00 | 64,38 | 64,38 |
Tableau 1. Résultats des classifieurs pour la tâche 1.
Nous constatons que l’ensemble des classifieurs obtiennent des résultats significativement plus élevés que l’approche aléatoire. Les meilleures performances sont obtenues par le réseau de neurones, suivi par le classifieur de type RandomForest. En observant les résultats, nous constatons que RandomForest se distingue par son comportement plus conservateur, dans le sens où l’algorithme minimise les faux positifs. La matrice de confusion, en Figure 1, illustre ce phénomène : la plupart des erreurs sont des faux négatifs, ce qui, typiquement, est considéré comme une erreur moins nuisible que son inverse.
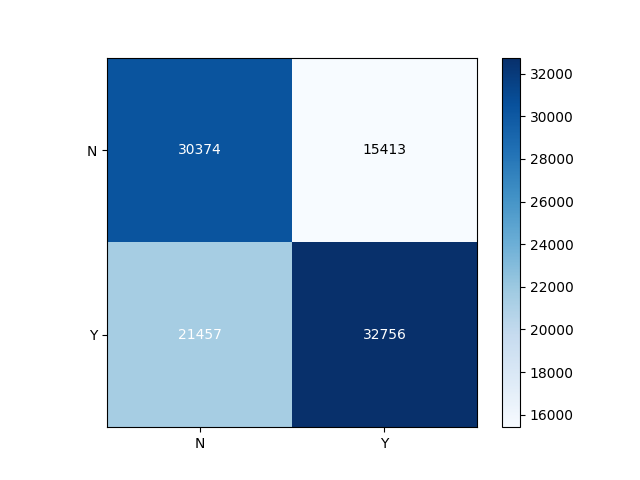
Figure 1. Résultats de l’algorithme Forêt d’Arbres Décisionnels. L’axe vertical correspond à la référence, l’axe horizontal aux prédictions.
Prédire le nombre d’offres d’un marché
Pour la prédiction du nombre d’offres, nous testons les algorithmes de régression détaillés à la section précédente. Les résultats obtenus sont rapportés au Tableau 2.
| MAE | RMSE | RMSLE | |
| Aléatoire | 17,66 | 29,37 | 1,76 |
| Médiane | 5,20 | 25,42 | 0,82 |
| SGD | 4,98 | 17,90 | 0,83 |
| NeuralNet | 5,03 | 17,22 | 0,79 |
| Ridge | 5,95 | 19,03 | 0,89 |
| Lasso | 5,26 | 18,47 | 0,88 |
Tableau 2. Résultats pour la tâche 2.
Les résultats mitigés des algorithmes de régression par rapport à la simple approche médiane montrent qu’il est difficile d’anticiper le nombre d’offres à partir des données disponibles. Les meilleurs résultats, ceux obtenus par le réseau de neurones et ceux obtenus par descente de gradient, restent assez proches des résultats de la médiane. Ridge et Lasso obtiennent même des résultats inférieures à la médiane selon la métrique MAE.
Prédir le montant d’un marché
On constate que, contrairement aux nombres d’offres, les montants sont extrêmement variés et la courbe des valeurs correspond presque à une courbe exponentielle double. Tenter d’utiliser ces valeurs telles quelles produit de très mauvais résultats. La Figure 2 représente les prédictions, en bleu, et la courbe de la référence, en vert. La ligne jaune correspond à la médiane.
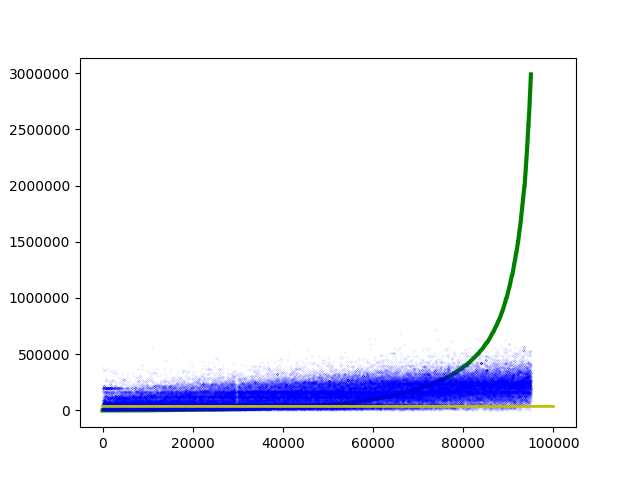
Figure 2. Prédictions (Ridge) et courbe de référence pour la prédiction du montant des marchés.
Par conséquent, pour la phase d’entraînement nous utilisons le logarithme des valeurs pour l’entraînement des modèles. Au moment du calcul des scores, nous utilisons l’exponentielle de la valeur prédite pour le comparer à la valeur de référence.
Les résultats obtenus sont rapportés au Tableau 3.
| MAE (Mil.) |
RMSE (Mil.) |
RMSLE | |
| Aléatoire | 3.77 | 31.58 | 3.71 |
| Médiane | 2.15 | 24.45 | 2.63 |
| SGD | 1.11 | 14.05 | 2.15 |
| NeuralNet | 1.11 | 13.96 | 2.13 |
| Ridge | 1.11 | 13.98 | 2.12 |
| Lasso | 1.14 | 14.08 | 2.54 |
Tableau 3 : résultats pour la tâche 3.
Le réseau de neurones ainsi que le régresseur Ridge obtiennent les meilleurs résultats. Cependant, les ordres de grandeurs des taux d’erreur sont extrêmement elevés : le meilleur RMSE obtenu étant supérieur à 13 millions.
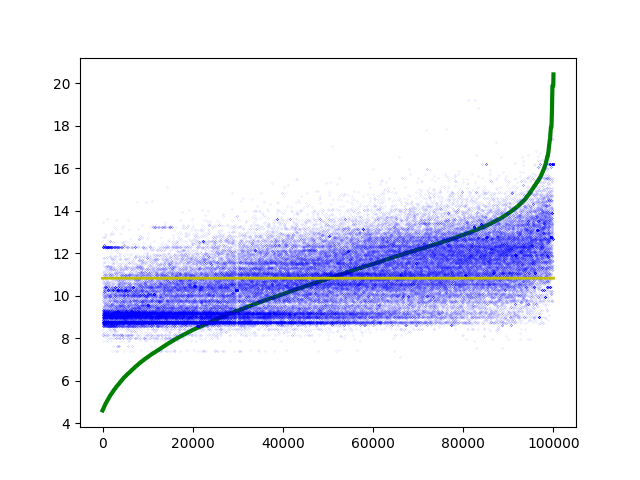
Figure 3. Prédictions (Ridge) et courbe de référence logarithmique pour la prédiction du montant des marchés.
La Figure 3 représente les résultats obtenus par une régularisation de Tikhonov à une échelle logarithmique. Le nuage des prédictions suit suffisament la courbe pour indiquer que les données permettent un apprentissage, mais une grande partie des résultats obtenus demeure éloignée de la référence par plusieurs ordres de grandeur.
Conclusion
Les résultats obtenus semblent favoriser l’usage de réseaux de neurones profonds, à la fois pour les tâches de classification des marchés selon la capacité des PME à les remporter, et pour les tâches de régression, i.e. pour prédire le nombre d’offres qui seront reçues, et prédire le montant du marché.
Les données employées présentent cependant un certain nombre de limites qui affectent significativement la qualité des modèles qu’ils peuvent servir à entraîner, ainsi que, par voie de conséquence, les conclusions qui peuvent être tirées de leurs résultats.
Pour améliorer les résultats des algorithmes et être en meilleur mesure de répondre aux questions posées par le challenge, il nous paraît également important de faire appel aux données textuelles associées aux avis de marché : son titre, en premier lieu, mais également la description qui lui est associée. En effet, des expériences préliminaires sur des données extraites de marchés publics ont montré que la simple utilisation de techniques de traitement automatique du langage naturel sur ces données textuelles permettait de prédire le montant des marchés avec une précision nettement plus robuste qu’en utilisant toutes les autres variables combinées.
Bibliographie
Weiss, S. M., & Kulikowski, C. A. (1991). Computer systems that learn: classification and prediction methods from statistics, neural nets, machine learning, and expert systems. Morgan Kaufmann Publishers Inc.
Chai, T., & Draxler, R. R. (2014). Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geoscientific model development, 7(3), 1247-1250.
Zhang, H. (2004). The optimality of naive Bayes. AA, 1(2), 3.
Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32.
Cortes, C., & Vapnik, V. (1995). Support-vector networks. Machine learning, 20(3), 273-297.
Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization.
Zhang, T. (2004, July). Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the twenty-first international conference on Machine learning (p. 116). ACM.
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 267-288.
Phillips, D. L. (1962). A technique for the numerical solution of certain integral equations of the first kind. Journal of the ACM (JACM), 9(1), 84-97.
il ne peut pas avoir d'altmétriques.)
