Citation
Les auteurs
Papa MBAYE
(papaaliounemeissa.mbaye@gmail.com) - Laboratoire de Recherche Missioneo - Freeland. Laboratoire de Mathématiques Blaise Pascal, UMR 6620 CNRS / Université Clermont AuvergneJean-Yves Ottmann
(jean-yves.ottmann@missioneo.fr) - Université Paris-Dauphine PSLSiavash ATARODI
(atarodi_sia@yahoo.fr) - Laboratoire Missioneo, Freeland group - ORCID : https://orcid.org/0000-0002-1882-2657
Copyright
Déclaration d'intérêts
Financements
Aperçu
Contenu
Introduction
Le traitement des données financières et internes à l’entreprise permet de prévoir. La prédiction a évidemment d’importants enjeux en finance, mais aussi pour les arbitrages [Kibekbaev et Duman, 2016] tout comme pour le pilotage des opérations [Cheng et Roy, 2011], et pour le pilotage comptable et gestionnaire global d’une entreprise (notamment l’établissement du budget de fonctionnement) [Barth et al., 2001].
Le portage salarial est un statut juridique particulier permettant d’exercer une activité professionnelle indépendante dans un cadre juridique de salariat de droit privé. Il constitue une forme d’emploi typique, basée sur une relation tripartite entre un client, un travailleur indépendant et une entreprise de portage salarial [Loufrani, 2015].
Cette étude de cas est intéressante pour évaluer la manière dont les indicateurs macro-économiques de l’INSEE peuvent être prédictifs avec une certaine anticipation du volume d’affaires à venir dans certains secteurs. Pour les entreprises de ce secteur, il y a donc une double difficulté à prévoir (ou prédire) leur Chiffre d’Affaires (CA). Il sera en effet dépendant de leur nombre de client (le nombre d’indépendants portés qui vont préférer l’entreprise à ses concurrentes, mais aussi à d’autres statuts juridiques comme la SASU ou la microentreprise), mais aussi de la performance économique de ses clients (qui peut être liée à des variables individuelles ou contextuelles). Il semble donc pertinent de voir si, pour cette activité spécifique, des indicateurs internes et externes peuvent permettre de prédire le CA et plus particulièrement si certains indicateurs macro-économiques peuvent être utilisés pour cela, à l’image de ce qui a été réalisé précédemment par d’autres auteurs [Sagaert et al., 2018,Sagaert et al., 2019]. Il s’agit dans la présente étude d’utiliser les indices de production dans les services mis à disposition par l’INSEE, dans le but de compléter les données internes disponibles pour la prévision du CA des entreprises du secteur du portage salarial. Ces indices macroéconomiques permettraient d’intégrer le contexte et les fluctuations du marché susceptibles d’influencer le CA à un horizon de trois à douze mois [Sagaert et al., 2019]. Derrière ce test, c’est bien entendu les possibilités d’automatisation de la prédiction qui sont intéressantes pour la gestion des entreprises [Verstraete et al., 2020].
L’accès aux données a été possible via le cadre de projets de recherche internes en contrôle de gestion et finances, dont certaines des conclusions et modèles sont utilisés dans le cadre du présent article, et notamment la mise en place de modèles de prévision du chiffre d’affaires. La recherche a été construite essentiellement sur les données d’une EPS, disponibles de 2012 à 2021, avec des résultats concluants. Deux modèles ont été testés : un modèle de lissage exponentiel et un modèle ARDL (Auto-Regressive distributed Lag). Le modèle ARDL semble par ailleurs offrir de meilleurs résultats.
1. Formulation du problème
L’objectif de cet article est de tester plusieurs modèles économétriques de prévision de CA pour des EPS (voir par exemple [Lim and McAleer, 2001, Sari et al., 2008]). Le CA se définit comme étant le produit du nombre de factureurs et du montant moyen de facturation.
$$ CA=\#Fact \times MMFact $$
Dans le modèle B, nous utiliserons les indicateurs macro-économiques de l’INSEE, attendu qu’on supposera que le marché du portage salarial est représentatif du secteur des travailleurs indépendants et des TPE du secteur des services aux entreprises.
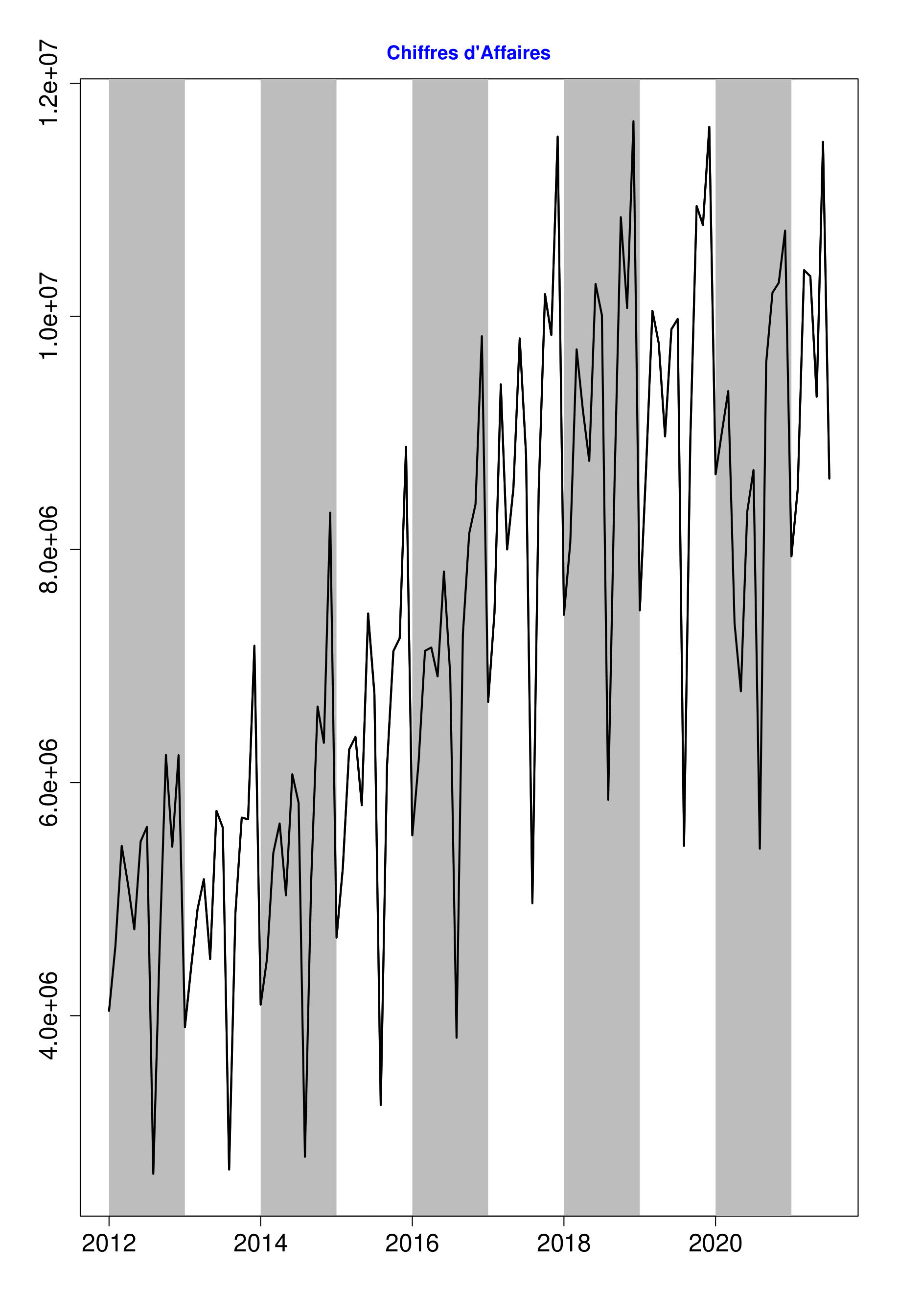
On note par \( Y_t \) la série temporelle qui représente le \( \textit{CA} \). Nous avons représenté à la \( Figure 1 \) un exemple d’évolution de CA de l’EPS. Dans cette figure, nous mettons la périodicité en évidence, graphiquement, avec des barres verticales. Nous remarquons une croissance dans le temps et un effet saisonnier marqué, mais aussi que l’importance de l’effet saisonnier augmente au fur et à mesure que les valeurs de la série augmentent. Ainsi \( Y_t \) sera représenté par un modèle multiplicatif défini comme suit :
$$ Y_t=C_t \times S_t + \epsilon_t $$
- \( C_t \) représente la tendance de la série : elle correspond à une évolution de long terme.
- \( S_t \) la saisonnalité : elle correspond aux comportements périodique qui se répètent à une fréquence.
- \( \epsilon_t \) le bruit : ou la partie aléatoire du processus.
Nous disposons de données internes à l’EPS, des données chronologiques qui dont nous verrons qu’elles ont plus ou moins d’influence sur l’activité au sein de cette EPS. Nous allons dès à présent énumérer quelques indices internes à l’EPS, que nous noterons par la suite les abréviations suivantes :
- \( \textit{Pros} \) : Le nombre de prospects de l’EPS.
- \( \textit{Recru} \) : Le nombre de consultants qui ont rejoint l’EPS.
- \( \textit{Fact} \) : Le nombre de consultants qui ont facturé.
- \( \textit{MMF} \) : Montant Moyen de Facturation.
L’évolution de ces indices est représentée à la Figure 2.
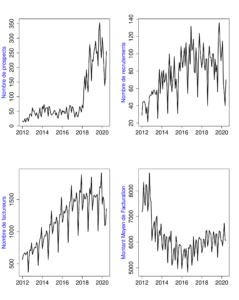
Mis à part ces indices internes à l’EPS, plusieurs indices de l’INSEE seront donc aussi utilisés comme possibles variables explicatives dans les modèles de régressions pour expliquer l’évolution du CA de l’EPS. Pour cette étude, nous nous sommes concentrés sur les indices en lien direct avec le secteur des services aux entreprises :
- \( \textit{Chômage} \) : Le taux de chômage (de toutes les personnes âgées de 25 ans au moins).
- \( \textit{ASAS} \) : Activités de Services Administratifs et de Soutien.
- \( \textit{ASST} \) : Activités Spécialisées Scientifiques et Techniques.
- \( \textit{IC} \) : Information et Communication.
- \( \textit{SSE} \) : Service de Soutien aux Entreprises.
2. Applications
2.1. Modèle A : par lissage exponentiel
Dans cette partie, nous allons appliquer les différents modèles présentés ci-dessus pour prédire le CA de ces EPS.
Rappelons que le modèle A fait abstraction des autres variables internes ou externes à l’entreprise. Ce modèle n’a comme information que les CA précédents pour prédire les CA futurs (ou éventuellement d’autres indicateurs, mais là encore prédits par eux-mêmes). Il semblerait toutefois plus judicieux d’avoir un modèle qui prend en compte plusieurs indices, et notamment des indices externes. En effet, on peut supposer que ces autres variables apporteront des informations complémentaires sur le climat des affaires des entreprises ou sur les dynamiques internes de chacune des entités – la crise du Covid ayant montré l’importance de ne pas se baser uniquement sur des modèles supposant une inertie totale des évolutions. De ce constat, on peut faire l’hypothèse de l’utilité du modèle B.
\( \textbf{Prévision du chiffre d’affaires de l’année 2019 en utilisant le modèle A} \)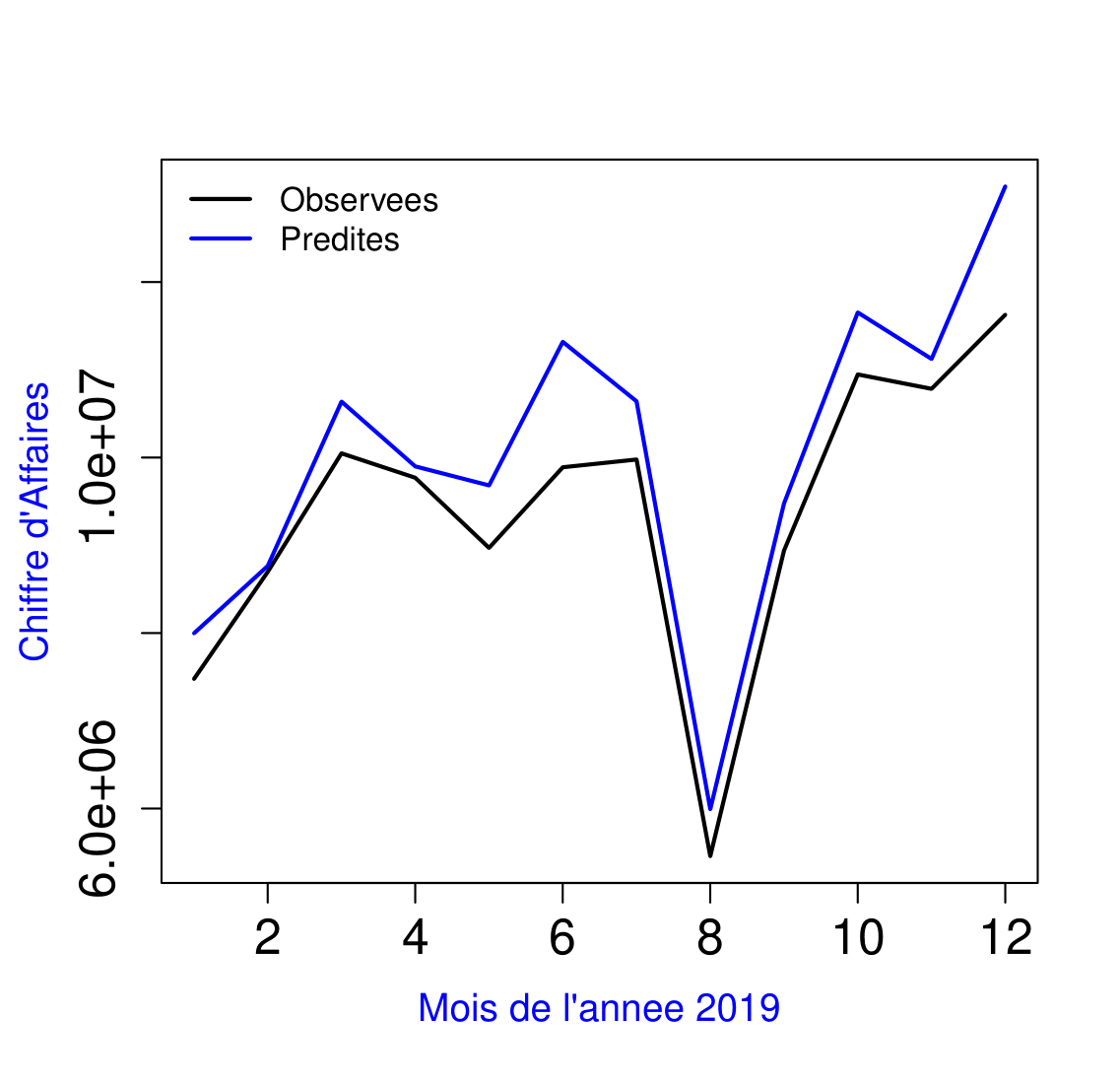
Avec le modèle A ci-dessus, nous obtenons un taux d’erreur de 7 %.
2.2. Modèle B : ARDL
2.2.1. Test de causalité
Comme nous disposons de plusieurs covariables, nous allons d’abord tester la stationnarité des séries grâce au test de Dickey-Fuller Augmenté ([Said et Dickey, 1984]; [Banerjee et al., 1993]). Pour vérifier si les séries sont stationnaires, nous avons utilisé la fonction \( adf.test() \) du package \( \textit{tseries} \) du logiciel R. Les tests de causalité de Granger donnent ces résultats :
| SSE | Pro | Rec | Fac | MMF | CA | |
| SSE | 1 *** | 1 *** | 5 *** | 4 * | 5 *** | |
| Pro | 1 *** | 7 * | 1 * | 2 * | 1 * | |
| Rec | 1 * | 7 * | 1 * | 5 * | 1 * | |
| Fac | 1 *** | 2 *** | 3 * | 1 ** | 1 ** |
Le chiffre dans le tableau ci-dessus représente le nombre de mois à partir duquel la variable explicative cause la variable à expliquer. En ligne, nous avons les variables exogènes et en colonne les variables endogènes. Les étoiles après les chiffres représentent la significativité de la p-value. On considère qu’il y a causalité d’une variable exogène sur une variable endogène si la p-value du test est inférieure à 0.05.
Concernant les indicateurs externes, le test ADF montre une causalité de l’indice SSE sur le nombre de factureurs 5 mois après (donc par conséquent, la valeur actuelle du SSE aura une influence sur le CA 5 mois plus tard). On constate aussi que le nombre de factureurs a une influence sur le montant moyen de facturation du mois suivant. Les indices ASAS, ASST et IC n’ont pas présenté de résultat concluant et ne sont donc pas intégrés à ce tableau, ni exploité dans la suite des analyses.
Enfin, on constate que les indicateurs internes de l’entreprise (nombre de prospects, nombres de factureurs, CA total) semblent avoir une influence forte sur l’indice SSE de l’INSEE du mois suivant. Cela montre que le portage salarial est un secteur représentatif du service aux entreprises et suggère que son étude permet l’étude des dynamiques macro-économiques de ces champs.
2.2.2. Application du modèle
Comme nous l’avons présenté précédemment, nous disposons ici d’un modèle de régression de séries temporelles. En effet nous allons prédire la variable à expliquer grâce aux données antérieures de cette variable, de la variable explicative, et des retards de la variable explicative. Ces paramètres doivent-être optimisés :
- r : le retard de la variable à expliquer à inclure dans le modèle (Voir l’équation 8 de la note
méthodologique) - l : le retard de la variable explicative à inclure dans le modèle (Voir l’équation 8 de la note
méthodologique)
Le jeu de données a été divisé en base d’apprentissage, base de validation et base test. Nous appliquons modèle sur les données de l’EPS. Pour faire une prévision de l’année \( S ( S \in {2017, 2018, 2019}) \), les données de notre base d’apprentissage sont les données de janvier 2012 à décembre de l’année \( S − 3 \). Pour la base de validation nous utilisons les données de janvier de l’année \( S − 2 \) à décembre de l’année \( S − 1 \). Les paramètres optimaux seront retenus grâce donc à la base de validation. Le package \( dLagM \) du logiciel \( R \) a été utilisé pour implémenter le modèle B.
Nous représentons dans la figure 5 ci-dessous le résultat des prévisions de CA pour l’année 2019, obtenues en utilisant comme variable explicative \( \#Fact. \)
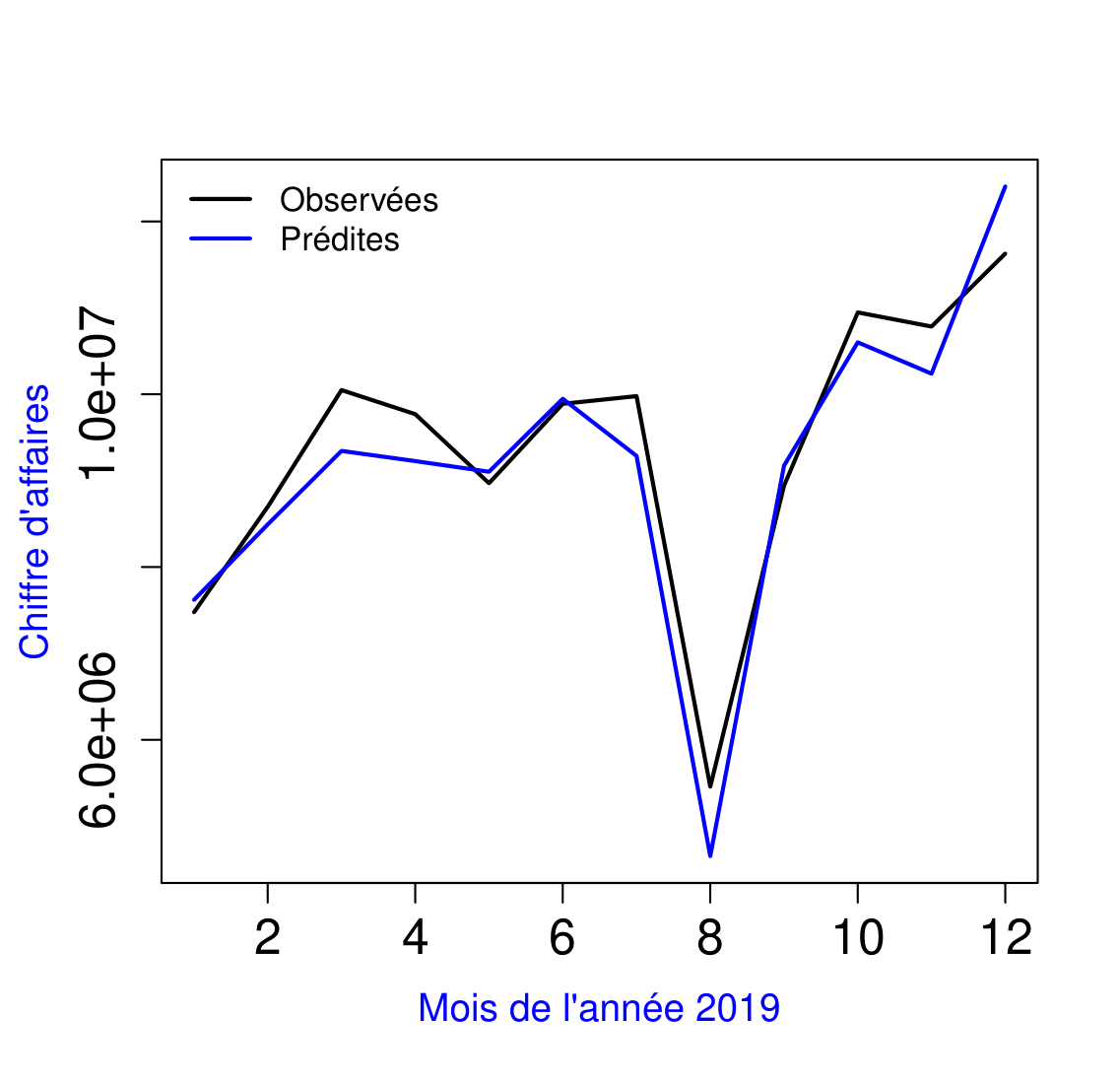
Le modèle B ci-dessous, nous obtenons un taux d’erreur de 2%. Le nombre de factureurs a été utilisé comme variable exogène.
Conclusion
Le modèle Holt-Winters (modèle A) présente de bons résultats, ce qui semble cohérent avec une activité qui présente d’importantes variations saisonnières et pour des entreprises qui présentaient une croissance particulièrement régulière. Par ailleurs, l’intérêt du modèle ARDL (modèle B) est la prise en compte d’autres indicateurs et de ne pas se résumer à une simple <<auto-prédiction>>. L’intégration des périodes COVID et post-COVID à nos analyses vont d’ailleurs dans le sens de privilégier ces modèles.
On constate par ailleurs l’intérêt d’intégrer des indices externes pour prédire des données internes [Verstraete et al., 2020]. Dans notre cas d’étude, l’indice SSE de l’INSEE permet une bonne prédiction de l’activité économique à venir dans le champ du service aux entreprises, et plus précisément le chiffre d’affaires à venir des entreprises de portage salarial. Bien que non développé dans cet article, il semblerait que le CA d’une grosse entreprise de portage salarial pourrait prédire le SSE des mois à venir. On retiendra aussi que des indices sont meilleurs prédicteurs quand il s’agit de faire une prévision à court terme et d’autres pour faire des prévisions à long terme.
On perçoit donc le potentiel d’usage de méthode de mathématiques appliquées ou d’économétrie pour des enjeux de contrôle de gestion. La frontière entre la prédiction et la prévision devient plus fine à l’aune des possibilités offertes par ces disciplines, et ouvre un champ de réflexion tant théorique que pratique sur l’usage des données internes, par exemple, les missions du contrôle de gestion au sein d’une organisation. On perçoit par ailleurs l’enjeu récursif : si les données internes de l’entreprise servent à prédire via des approches algorithmiques, et donc à prendre des décisions, la qualité, la robustesse et la disponibilité de ces données internes deviennent d’autant plus importante. Le croisement de données « financières » classiques (comme le CA) et de données issues des opérations (dans ce cas d’étude, par exemple, le nombre de prospects), démultiplie ces enjeux.
Bibliographie
Banerjee, A., Dolado, J. J., Galbraith, J. W., & Hendry, D. (1993). Co-integration, error correction, and the econometric analysis of non-stationary data. Oxford university press.
Barth, M. E., Cram, D. P., & Nelson, K. K. (2001). Accruals and the prediction of future cash flows. The accounting review, 76(1), 27-58.
Cheng, M. Y., & Roy, A. F. (2011). Evolutionary fuzzy decision model for cash flow prediction using time-dependent support vector machines. International journal of project management, 29(1), 56-65.
Kibekbaev, A. and Duman, E. (2016). Benchmarking regression algorithms for income prediction modeling. Information Systems, 61:40–52.
Lim, C., & McAleer, M. (2001). Forecasting tourist arrivals. Annals of tourism research, 28(4), 965-977.
Loufrani, Y. (2015). Le portage salarial enfin sécurisé. Revue française de comptabilité, 488, 7-8
Sagaert, Y. R., Aghezzaf, E. H., Kourentzes, N., & Desmet, B. (2018). Tactical sales forecasting using a very large set of macroeconomic indicators. European Journal of Operational Research, 264(2), 558-569.
Sagaert, Y. R., Kourentzes, N., De Vuyst, S., Aghezzaf, E. H., & Desmet, B. (2019). Incorporating macroeconomic leading indicators in tactical capacity planning. International Journal of Production Economics, 209, 12-19.
Said, S. E., & Dickey, D. A. (1984). Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika, 71(3), 599-607.
Sari, R., Ewing, B. T., & Soytas, U. (2008). The relationship between disaggregate energy consumption and industrial production in the United States: an ARDL approach. Energy Economics, 30(5), 2302-2313.
Verstraete, G., Aghezzaf, E. H., & Desmet, B. (2020). A leading macroeconomic indicators’ based framework to automatically generate tactical sales forecasts. Computers & Industrial Engineering, 139, 106169.
Annexes
il ne peut pas avoir d'altmétriques.)
