Les forêts aléatoires

L’algorithme des forêts aléatoires (Breiman, 2001), également connu sous le nom de « Random Forest », est une version ensembliste des arbres de classification. Il consiste, par l’agrégation de plusieurs arbres, à améliorer les capacités prédictives d’un modèle par arbre de classification jugé trop instable.

Selon Breiman, les performances de prédiction d’une forêt aléatoire dépendent de deux paramètres : la qualité de prédiction de chaque arbre et leur indépendance. Ainsi, afin de rendre les arbres plus indépendants tout en préservant leur qualité de prédiction, Breiman propose deux types de perturbations :

• La construction des différents arbres ne se fait pas sur l’échantillon d’apprentissage total, mais sur des sous-échantillons aléatoires de ce dernier (méthode de rééchantillonnage bootstrap)
• La meilleure division d’un nœud n’est pas choisie en testant l’ensemble des variables explicatives, mais une partie seulement de celles-ci, sélectionnée aléatoirement.

Cette double « randomisation » permet d’aboutir à des arbres non corrélés. Chacun de ces arbres est moins performant qu’un arbre construit par méthode classique (CART par exemple), mais le fait d’agréger ces arbres entre eux permet l’obtention de résultats très performants et plus stables.

Une fois la forêt aléatoire construite, elle permettra d’assigner à un individu quelconque, dont nous observons uniquement une suite de variables explicatives correspondant aux données qui caractérisent cet individu, sa valeur d’intérêt ou cible tout en minimisant les risques d’erreurs. Pour cela, le sujet est envoyé dans chacun des arbres de la forêt et classifié par ceux-ci dans un des groupes (A ou B dans l’exemple ci-dessous). On dit de façon imagée que l’arbre « vote » pour le groupe adapté au sujet. Le groupe le plus présent (le vote gagnant) est le groupe dans lequel la forêt classe l’individu (Figure 1).

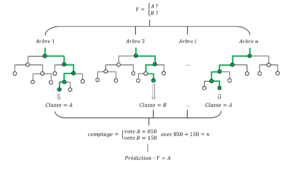
Figure 1 – Système de classification binaire (groupe A / groupe B) d’une forêt aléatoire

Jeu de données « Amazon Review Data »

Les données brutes

Dans ce travail, nous avons utilisé la base de données « Amazon Review Data » (Ni, 2018) qui contient un nombre important d’avis d’utilisateurs, recueillis sur le site Amazon, durant les 20 dernières années.  Les enregistrements sont stockés sous forme de fichiers JSON et contiennent des informations sur les utilisateurs ayant donné leur avis (variables « reviewerID » et « reviewerName »), les caractéristiques des différents produits concernés par les avis (catégorie, description, prix, marque, produits associés…) accessibles dans une base annexe grâce à l’ID produit (variable « asin »), les commentaires (variable « reviewText » et « summary »), leur utilité (variable « helpful »), les notes données par les consommateurs (variable « overall ») et les dates (variables « unixReviewTime » et  « reviewTime »).

Compte tenu de la taille importante du fichier total (environ 35 go) nous travaillerons sur un sous-ensemble de données comprenant uniquement les produits appartenant à la catégorie « Home and Kitchen ». De plus, afin de ne sélectionner que des avis fiables et pertinents, nous limitons les données aux enregistrements : complets, non atypiques (longueur du commentaire qui ne soit pas anormalement courte ou longue par exemple), ayant une utilité non nulle (utilisation de la variable « helpful ») et correspondant à des utilisateurs ayant laissé un minimum de 5 avis sur Amazon.

Traitement de la variable cible

L’objectif visé par cette application est la construction d’un modèle permettant de prédire une note, notre variable cible, en fonction des différentes variables explicatives à disposition telles que les commentaires, pseudos ou dates. Il existe deux options dans la considération de ce problème. Il peut être vu :

• Comme un problème de régression, si l’on considère que la note est une variable numérique continue sur l’intervalle [0 ;5] et si l’on cherche à prédire sa valeur exacte.
• Comme un problème de classification en groupes, si l’on considère que la note est une variable discrète et si l’on cherche à prédire sa classe (avec par exemple, pour  les valeurs possibles {1,2,3,4,5} ou encore pour , les valeurs possibles {négatif, neutre, positif}.

Nous optons ici pour l’option d’une classification binaire, en considérant un commentaire comme positif si la note est strictement supérieure à 3 et négatif si la note est inférieure ou égale à 3. Afin de garantir une qualité du modèle, il est important de veiller à ce que la distribution de la variable cible soit équilibrée. Dans notre cas, on observe une distribution des notes très déséquilibrée avec la modalité 5 sur-représentée par rapport aux autres modalités. Nous effectuons donc une phase de « redressement », qui consiste à modifier l’échantillon en fonction de la variable cible, par suppression aléatoire de profils sur-représentés, cela afin de s’assurer de la représentativité de chaque modalité.

Choix des variables explicatives

L’un des avantages des forêts aléatoires est qu’elles acceptent des données de toute nature (quantitative, qualitative, ordinale…). Cependant, comme de nombreux autres classifieurs, elles ne permettent pas de gérer les données non structurées telles que les commentaires.

Le problème des données non structurées est qu’elles sont « uniques » pour chaque individu (il y a autant de dimensions que d’individus) et n’ont donc, à l’état brut, qu’un faible pouvoir discriminant et aucune utilité pour un algorithme dont l’objectif est de repérer des similitudes entre les individus. Pour pallier cette problématique, la procédure courante consiste à extraire de ces données les seules caractéristiques les plus utiles afin d’en réduire les dimensions. Ce procédé, appelé « extraction d’information », peut être considéré comme le fait de compléter un formulaire ou remplir une base de données structurées à partir de textes libres. La difficulté réside dans le choix des champs qui composent cette base d’information. Il n’est pas défini par avance, mais dépend du contexte, des expériences cumulées et acquises par l’étude de différents cas ou encore de simples intuitions…

De nombreux auteurs se sont penchés sur ce sujet. Certains ont mis l’accent notamment sur l’importance de la négation dans un texte, d’autres sur l’utilisation de conjonctions de coordination ou encore sur la pertinence des adjectifs…

Après étude d’un panel de ces différentes approches, nous proposons dans ce travail les types de champs suivants :

Détection de termes pré-définis

Il s’agit ici de détecter la présence de caractères ou termes ayant, selon la littérature,  une importance significative. Nous nous limitons aux termes et caractères suivants : les signes de ponctuation, les conjonctions (and, or, but, either-or, et neither-nor), les négations (not, ‘t, never, nothing, hardly, nobody, nowhere, no + body…), les abréviations type « SMS » (recueillies par crowdsourcing) et les  termes, par catégories (noms, verbes, adjectifs et adverbes), identifiés comme les plus significatifs (présents dans un grand nombre de commentaires sans dépasser un certain seuil afin de garantir une valeur discriminante). La méthode et les procédures ont été analysées dans un précédent numéro de la revue Management et Data Science (Ghewy et al., 2019).

Structure générale du commentaire

Il s’agit de données relatives à la construction du commentaire telles que sa taille, son nombre de mots, son nombre de phrases, son nombre de caractères ou encore son ratio adjectif/verbe/nom/adverbe…

Détection des différents thèmes du corpus 

Il s’agit ici, dans un premier temps, de repérer les termes significativement liés, de les regrouper en plusieurs thèmes (par exemple les mots tels que parfait, agréable, content, génial… sont associés au thème 1) puis de décomposer chaque commentaire en une combinaison d’un ou plusieurs thèmes en fonction de la fréquence d’apparition de chaque thème dans le commentaire.

Nous avons utilisé pour cela la méthode LDA – Latent Dirichlet Allocation – (Blei et Al 2003) implémentée dans le package R « Text2vec » (Selivanov, 2020). Cette méthode, dont les différentes procédures ont été décrites dans un précédent article (Ghewy et al., 2019), permet, d’une part, d’identifier les différents thèmes et, d’autre part, d’attribuer à chaque mot sa probabilité d’appartenance à un thème.

Après plusieurs essais, nous nous sommes arrêtés sur les 7 thèmes suivants : un thème lié à la satisfaction, un thème lié à la conception, un thème lié à des problématiques d’utilisation, un thème lié à l’utilisation pratique, un thème lié au remplacement d’un ancien produit, un thème lié à des problématiques de capacité et un thème lié au rapport qualité/prix.

Détection des sentiments / émotions / opinions

L’objectif est d’attribuer un sentiment ou une émotion à un texte. Pour cela, la procédure courante consiste à utiliser des lexiques ou dictionnaires d’opinion qui répertorient différents mots porteurs d’opinions. En repérant ensuite la présence de ces mots dans les textes à analyser, il est possible, comme pour la détection de thèmes présentée dans le point précédent, d’attribuer un sentiment général à l’ensemble du texte.

On peut utiliser des lexiques existants ou bien les construire. Nous utilisons ici le support « nrc » (Saif et Turney, 2013), disponible sur R via le package « tidytext » (Silge et Robinson, 2020). Ce dictionnaire a été construit via le crowdsourcing, en utilisant notamment des données d’Amazon, de Twitter ou encore des critiques de restaurants ou de films. Il attribue à 6468 mots uniques un ou plusieurs des dix « sentiments » suivants : confiance, peur, scepticisme, tristesse, colère, surprise, enthousiasme, dégoût, joie ou anticipation. On travaille ici dans un cas simple sur mots uniques (« unigram »), mais il est également possible d’étudier les associations de mots (« Bigram », Trigram » ou « N-gram ») pour affiner les résultats.

Ainsi, nous avons présenté les différentes informations extraites de la variable commentaire (variable « reviewText »), mais d’autres champs, tels que la date (variable « reviewTime ») et le pseudo (variable « reviewerName ») ont également été utilisés. Il est en effet possible d’extraire du champ date, qui en l’état représente une faible valeur ajoutée, des informations plus riches et discriminantes telles que le jour, le mois ou la semaine. De même, une analyse sémantique de la variable pseudo, qui du fait de sa forte diversité ne présente aucune valeur à l’état brut, permet d’extraire des informations plus discriminantes telles que la structure (s’agit-il d’un {nom prénom} (« Martin Schwartz »), d’un {prénom} (« John ») ou bien d’un pseudo plus fantaisiste (« Tea Lover »)), le sexe ou l’âge de l’individu.

Après ces différentes opérations sur les 3 champs non structurés commentaire, pseudo et date, on obtient une base de données finale composée de plusieurs dizaines de variables explicatives structurées et adaptées aux contraintes des forêts aléatoires. Il est important de noter que les différentes variables qui composent cette base de données dépendent des appréciations de l’auteur, de la littérature et du contexte. Étant donné qu’il existe un grand nombre de variables pouvant potentiellement avoir un effet sur la cible et qu’elles ne peuvent être traitées de façon exhaustive, il est judicieux de faire évoluer cette base de données en testant de nouvelles variables afin de permettre aux algorithmes la découverte de liens, d’associations et de corrélations nouvelles.

Modélisation par forêts aléatoires

Conception du modèle

Pour construire notre modèle nous utilisons la librairie R « randomForest » (Liaw et Wiener) qui implémente la méthode des forêts aléatoires basée sur le code Fortran original de Breiman et Cutler (2003). La procédure R est la suivante :

library(randomForest)
# Création de la forêt aléatoire
RF = randomForest(CIBLE ~., data = bdd.app, ntree= 1000, na.action = na.roughfix)

Paramètres du modèle :

• La mention « CIBLE » correspond à notre variable cible binaire « Positif » / »Négatif »
• La base de données utilisée « bdd.app » correspond à notre base d’apprentissage constituée des différentes variables détaillées dans la section précédente;
• Les données manquantes ont été imputées par moyenne ou médiane en fonction de leur type (quantitative ou qualitative) grâce au paramètre « na.action = na.roughfix »;
• Le nombre d’arbres (paramètre « ntree ») a été fixé à un nombre raisonnable de 1000 arbres, pour maximiser les chances d’atteindre la convergence du modèle (Breiman, 2001) tout en réduisant les temps de calcul ;
• Les autres paramètres de la fonction « randomForest » (tels que le « mtry » ou le « nodesize ») ont été laissés par défaut.

Évaluation du modèle

Une fois le modèle construit, il convient de tester ses performances en estimant ses erreurs. Lorsque l’erreur associée au modèle est estimée à partir de l’échantillon d’apprentissage, elle est généralement sous-estimée car l’échantillon sert de base à la construction du modèle. Ainsi, pour calculer un taux d’erreur fiable, il est important de tester le modèle sur un échantillon aléatoire de données qui n’a pas servi à sa construction. Deux options s’offrent alors :

• Prendre en considération le fait que les arbres ayant servi à la construction de la forêt sont construits sur des sous-échantillons de l’échantillon d’apprentissage et, par conséquent, n’utilisent pas toutes les observations de celui-ci. Si l’on considère les données restantes, on utilise alors la méthode « Out Of Bag » (OOB), implémentée dans la fonction « randomForest » et qui donne dans notre application un taux d’erreur de 23.83%.
• Créer manuellement un échantillon aléatoire de données qui n’a pas servi à la construction du modèle. Cet échantillon, appelé échantillon « test », comprend les mêmes variables que l’échantillon d’apprentissage, mais des individus différents. Dans notre application, nous créons un échantillon test composé de 20000 individus , 9910 négatifs et 10090 positifs. Les résultats obtenus après déploiement du modèle « RF » sur cette base de données test nous permettent d’obtenir la matrice de confusion suivante :

# Déploiement, comparaisons avec la réalité, création mat. conf.
pred <- predict(RF,newdata=bdd.test,type="class")
matconf = table(pred,bdd.test$CIBLE)

# Calcul du taux de bonne classification
goodclass = sum(diag(matconf))/sum(matconf)

# Calcul du taux d'erreur
badclass = 1 - goodclass

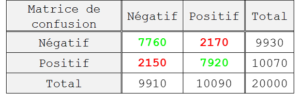
Le mode de construction de la matrice de confusion est simple : on supprime la variable réponse de l’échantillon test puis on demande au modèle de l’estimer (utilisation de la fonction R « predict »). Une fois les estimations réalisées, on compare les résultats avec les valeurs d’origine et on les classe dans la matrice de confusion. Les lignes correspondent aux prédictions tandis que les colonnes correspondent à la réalité. À partir de cette matrice de confusion, nous pouvons calculer le taux de bonne classification (ou le taux d’erreur), qui correspond au taux de bonne (ou mauvaise) correspondance entre les résultats du modèle et les résultats observés dans la réalité. On a ici un taux de bonne classification de 78.40%. Ce taux signifie que, dans 78,40% des cas, le modèle a donné une réponse en accord avec la réalité observée. Pour avoir une idée de comparaison, attribuer une prédiction au hasard à chaque individu (par pile ou face par exemple) donnerait, dans le cas où les modalités de la variable cible sont équilibrées (comme c’est le cas ici avec autant de commentaires positifs que négatifs dans l’échantillon) un taux de bonne classification de 50%.

Le taux de bonne classification peut être décomposé en nombreux indicateurs tels que le taux de « vrais positifs », aussi appelé « sensibilité » ou « recall » (individus positifs bien classés parmi l’ensemble des individus positifs), le taux de « vrais négatifs », ou « spécificité » (individus négatifs bien classés parmi l’ensemble des individus négatifs) ou encore la « précision » (individus positifs bien classés parmi l’ensemble des individus prédits comme positifs). Ce n’est que si l’ensemble de ces indicateurs est élevé que le modèle peut être considéré de bonne qualité. Ces indicateurs peuvent être lus dans la matrice de confusion (on a ici une sensibilité de 78.65%, une spécificité de 78.15% et une précision de 78,49%) ou représentés sur une courbe ROC (Figure 2).

library(ROCR)
# Prédiction sous forme de probabilité et comparaison avec la réalité
pred.prob <- predict(RF, newdata = bdd.test, type = "prob")
pred1 <- prediction(pred.prob[, 2], bdd.test$CIBLE)

# Taux de vrais positifs faux positifs
perf1 <- performance(pred1, "tpr", "fpr")

# Traçage de la courbe ROC / droite égalitaire / Courbe Optimale
plot(perf1, col = "blue",xlab="Tx fx pos.",ylab="Tx vrais pos.",lwd=2)
abline(a = 0, b = 1, col = "red",lwd=2)#Droite egalitaire
par(new=TRUE)
plot(c(0,0,1), c(0,1,1),col="limegreen",type="l",bty="n",lwd=2)

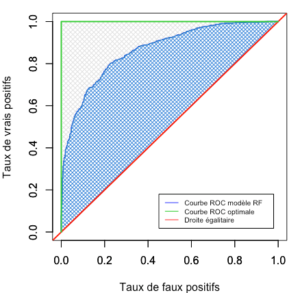
Figure 2 – Courbe ROC

Un classifieur optimal, qui ne se trompe jamais, donnera la courbe ROC représentée en vert sur le graphique ci-dessus (Figure 2). En revanche, un classifieur aux faibles performances (comparable à un pile ou face), donnera la courbe ROC en rouge. Ainsi, plus la courbe ROC est proche de la courbe verte, plus le classifieur est globalement bon. Dans le cas qui nous occupe, on observe une courbe ROC (en bleu) « bombée » (aire sous la courbe, hachurée en bleu, élevée) gage de qualité du classifieur. Le classifieur offre cependant une marge de progression, hachurée en gris sur le graphique.

L’ensemble des résultats obtenus prouvent qu’il existe des corrélations significatives entre les variables explicatives que nous avons utilisées et la note. Ces liens permettront par la suite d’assigner à de nouveaux individus qui seront présentés au modèle leur valeur cible « note », simplement à partir de l’observation des trois champs commentaire, pseudo et date, avec une fiabilité de 78.40%.

Analyse de l’importance des variables

Outre leur utilité pratique pour effectuer des prédictions, les forêts aléatoires permettent de comprendre et d’expliquer les résultats d’une classification grâce à l’étude de l’importance des variables explicatives.

Nous considérerons ici la « mesure d’importance par permutation » proposée par Breiman (2001) qui stipule qu’une variable est considérée comme importante pour la prédiction si en brisant le lien entre cette variable et la variable cible l’erreur de prédiction augmente. Cette méthode est implémentée par la fonction « Importance » du package « randomForest ». La procédure est la suivante :

#Mesure d'importance (Brieman) + Représentation
rf.imp = importance(RF, type= 2)[order(importance(RF, type= 2), decreasing= T),]
barplot(rf.imp[1:25], col = gray(0:nrow(RF$importance) / nrow(RF$importance)),ylim = c(0,300),ylab = 'Importance', cex.names = 0.6, las = 3)

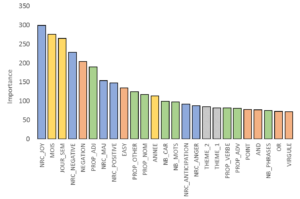
Figure 3 – Représentation de la contribution des 25 variables les plus importantes

Cette mesure d’importance, caractéristique des forêts aléatoires, est très intéressante au plan analytique car elle nous renseigne sur la contribution des différentes variables explicatives à la modélisation et nous permet de mieux comprendre la cible cassant ainsi l’effet « boite noire » qui accompagne souvent les différents algorithmes de machine learning. On remarque par exemple ici (Figure 3):

• Une forte contribution des variables de sentiments, démontrant la pertinence du dictionnaire « NRC »,
• Une forte contribution des variables extraites du champ « date »,
• Une forte contribution des données relatives à la structure du commentaire (proportion d’adjectifs ou de noms) ainsi qu’à sa taille (nombre de caractères ou de mots),
• Une forte contribution de certains termes pré-définis tels que la négation, la ponctuation ou le mot « EASY ».
• Une contribution relativement faible des variables correspondantes aux 7 thèmes déterminés par méthode LDA (rang 17 pour le thème 2 et 18 pour le thème 1),
• Enfin, une absence de contribution de certaines variables (comme les variables relatives à la structure du pseudo ou à l’utilisation de mots pré-définis tels que « Made », « Small », « New »…). Ces variables pourront éventuellement être supprimées et remplacées par d’autres variables.

Il est important de noter, pour conclure cette partie, que la mesure d’importance, telle qu’elle est proposée par Breiman, nous renseigne sur l’importance des variables une à une, mais ne permet pas de mesurer des importances conditionnées à d’autres variables. La présence d’un mot particulier par exemple peut n’avoir aucune importance sur un grand nombre de commentaires, mais une importance élevée sur un sous-échantillon de commentaires comme ceux très courts.

Conclusion et perspectives d’améliorations

L’objectif de cet article était de construire un modèle de classification permettant, à partir de différentes informations relatives à un commentaire, de prédire et d’expliquer une note attribuée par un consommateur pour un produit donné. Nous avons pour cela utilisé la méthode des forêts aléatoires qui nous a conduit à l’obtention d’un modèle avec une fiabilité de 78.40%. Ce résultat prouve qu’il existe des corrélations significatives entre un texte et une note. Afin d’approfondir ce résultat, nous avons utilisé une mesure d’importance des variables qui nous a permis d’identifier les variables qui contribuaient le plus à la classification. Nous avons ainsi pu observer une forte contribution, assez logique, des variables de sentiment, mais également une contribution plus étonnante de variables relatives à la structure du commentaire tel que sa taille, la ponctuation et la nature des mots qui le compose.

Le modèle que nous avons proposé présente de larges perspectives d’évolution. Le taux de bonne classification de 78.40% que nous avons obtenu peut être amélioré encore. Pour cela, plusieurs pistes de réflexion sont envisageables :

• Une analyse des sentiments en considérant une approche « n-gram » (« bigram », « trigram »…) plutôt qu’une approche « unigram » comme nous l’avons choisie ici.
• Des modifications dans le processus d’identification et d’intégration des thèmes. Comme nous avons pu le voir, la contribution des différentes variables relatives aux 7 thèmes identifiés par méthode LDA est faible (rang 17 pour le thème le plus significatif). Le choix du nombre de thèmes ou la méthode d’intégration par proportion sont peut-être à reconsidérer.
• La mise en place d’une boucle de valeur des données. Comme nous avons pu le voir avec la procédure d’analyse des variables importantes, il peut arriver que certaines données n’aient qu’un faible pouvoir prédictif (voir aucun) sur la cible visée. L’intégration de ces données, dans des proportions trop importantes, peut alors avoir des conséquences négatives sur les analyses (augmentation des temps de calculs ou de la variabilité des modèles). Il est donc important d’ajouter dans le processus d’analyse que nous avons proposé, une phase de sélection intelligente des variables, sous forme de boucle itérative, qui, suite à l’analyse a posteriori des variables importantes, conserverait automatiquement les variables les plus significatives et supprimerait les moins pertinentes. Les variables supprimées pourront être remplacées par de nouvelles (mots prédéfinis, structure du commentaire, dictionnaires d’opinions) qui seront à leur tour évaluées lors des prochaines itérations de la boucle.