Heuristique vs. Stochastique pour l'Exploration des Hyperparamètres

En raison de son fondement probabiliste et de sa structure formelle basée sur la théorie des probabilités et de la décision, l'optimisation bayésienne (BO) est un algorithme stochastique alors que le CMA-ES combine une méthode stochastique pour la génération et l'évaluation et une heuristique pour la sélection des solutions candidates.

Les méthodes heuristiques peuvent être utiles pour réduire l'espace de recherche et guider la recherche vers des régions prometteuses.

Illustrons cette dernière observation avec un exemple. Supposons que nous voulions trouver un nombre entier entre 1 et 1000, et nous avons deux approches pour le faire :

Approche Heuristique : Nous utilisons une méthode heuristique qui divise itérativement l'intervalle en deux moitiés et sélectionne la moitié qui contient la cible jusqu'à ce que nous la trouvions:

Approche Stochastique : Nous utilisons une méthode stochastique qui sélectionne un nombre au hasard dans l'intervalle et vérifie s'il s'agit de la cible. Si ce n'est pas le cas, elle répète ce processus jusqu'à trouver la cible:

Dans la plupart des cas, l'approche heuristique sera plus rapide et efficace pour résoudre ce problème spécifique en réduisant l'espace de recherche de manière systématique:

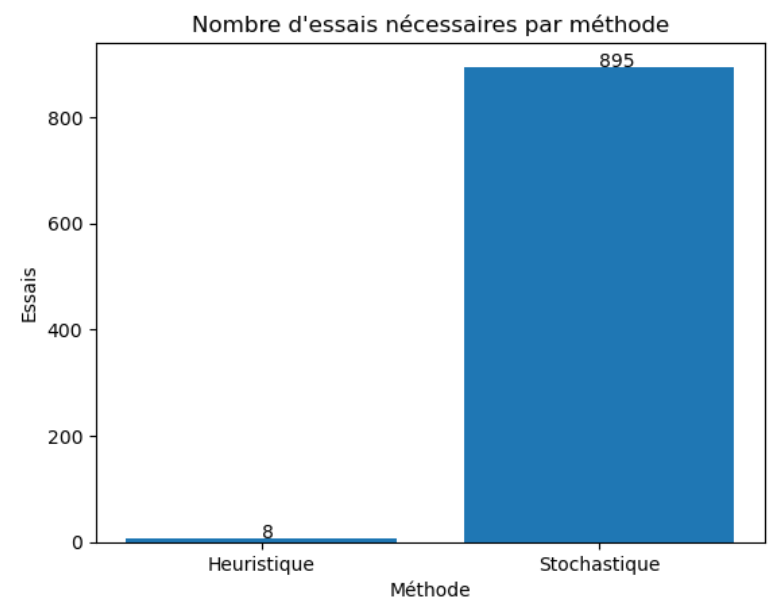
Cela dit, l'efficacité de la méthode d'exploration de l'espace des hyperparamètres dépend essentiellement de la caractéristiques de la fonction objectif. La convexité est une caractéristique souhaitable car elle garantit l'unicité du minimum global. Cependant, dans de nombreux problèmes de machine learning, les fonctions objectif sont non convexes en raison de la complexité des modèles.

Les fonctions objectif non convexes peuvent avoir des crêtes locales, c'est-à-dire des minima locaux qui ne sont pas le minimum global. Cela peut rendre l'optimisation plus difficile.

La fonction de Rosenbrock est une fonction d'optimisation bien connue utilisée pour tester les algorithmes d'optimisation. Elle est définie comme suit :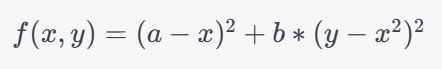

où a et b sont des constantes. La valeur typique de ces constantes est $a=1$ et b=100.

Le minimum global de la fonction de Rosenbrock est situé à $x=1$ et $y=1$, et la valeur de la fonction à ce minimum est f(1,1) = 0. La présence de  minima locaux et de crêtes locales est ce qui rend la fonction de Rosenbrock un défi pour les algorithmes d'optimisation. Ils peuvent entraîner une convergence vers un minimum local au lieu du minimum global souhaité si l'algorithme d'optimisation n'est pas capable de les surmonter.

Ci dessous les trajectoires d'optimisation et le mimimum de cette fonction trouvé avec les algorithmes CMA-ES et Hyperopt:

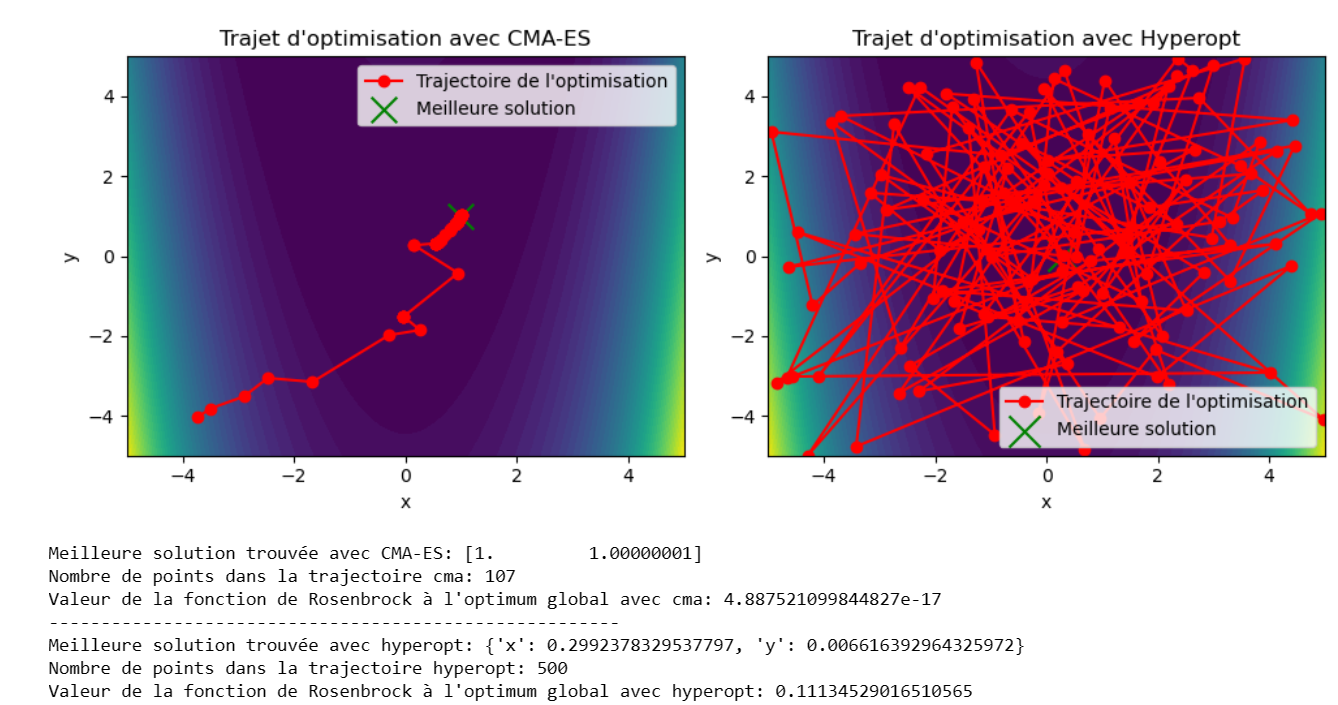
Remarquons d'abord que CMA-ES est plus proche du minimum en 107 évaluations contre 500 coté Hyperopt! Mais le plus frappant est la manière dont le CMA-ES explore de manière bien plus efficace l'espace des hyperparamètres. Comme on l'a vu en partie 1, le CMA-ES maintient une estimation de la covariance des solutions, ce qui lui permet de s'adapter aux propriétés locales de la fonction. Dans le cas de la fonction de Rosenbrock, qui a une forme allongée et étroite, le CMA-ES peut ajuster la covariance de manière à explorer plus efficacement cette structure, ce qui rend la convergence plus rapide.

La mise à jour de la covariance permet de se diriger vers les régions les plus prometteuses comme le montre le graphique ce dessous:

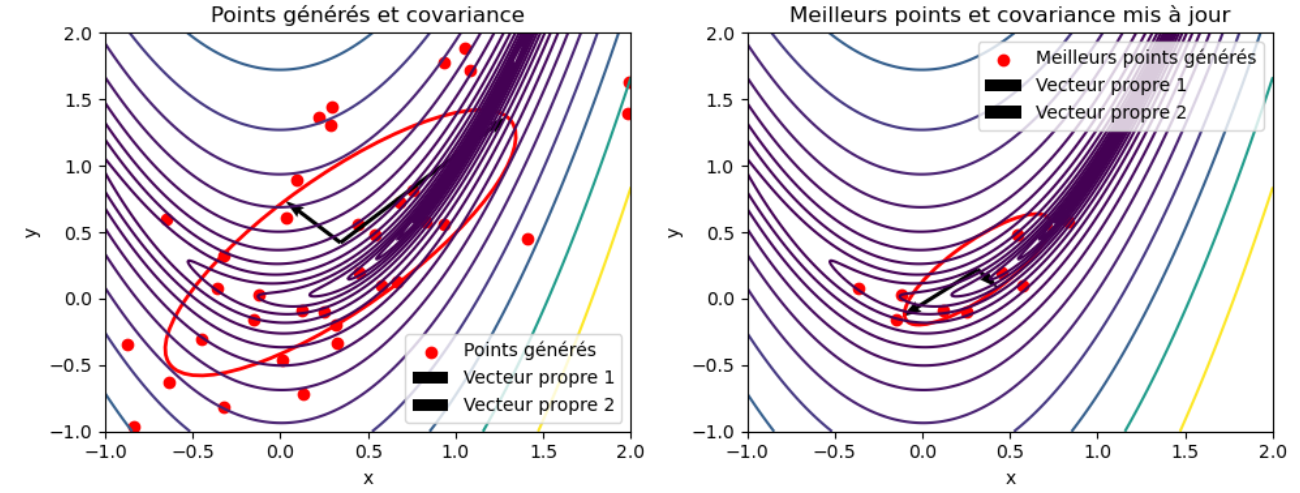
Les vecteurs propres de la matrice de covariance indiquent les directions principales le long desquelles les données sont dispersées.

Plus précisément :

1. Les vecteurs propres (de la matrice de covariance): Ce sont des vecteurs unitaires qui définissent des directions dans l'espace. Chaque vecteur propre est associé à une valeur propre correspondante.
2. Les valeurs propres (de la matrice de covariance) : Ce sont des valeurs numériques qui mesurent la variabilité le long des directions définies par les vecteurs propres. Plus la valeur propre est grande, plus la dispersion des données le long de cette direction est importante.

Ainsi, sur le graphique de gauche, une centaine de points sont d'abord générés via une loi normale multivariée. Les meilleurs points sont alors sélectionnés et la matrice de covariance mise à jour à partir de ceux ci. L'algorithme utilise la nouvelle matrice de covariance pour générer de nouvelles solutions candidates et mettre à jour la covariance (graphique de droite). Les directions où la covariance est grande (c'est-à-dire les directions où la fonction varie le plus) auront des pas plus grands, tandis que les directions où la covariance est petite auront des pas plus petits.

En résumé, le CMA adapte sa direction et sa vitesse de convergence vers le point optimal, tandis que l'optimisation bayésienne ne se dirige pas vers le point optimal mais sélectionne les points les plus prometteurs selon la probabilité d'amélioration, ce qui donne un avantage au CMA dans l'efficacité de l'exploration de l'espace des hyperparamètres.

Gestion des valeurs discrètes

L'optimisation bayésienne est principalement conçue pour l'optimisation d'hyperparamètres continus, mais elle peut également être adaptée pour gérer les hyperparamètres discrets. L'hyperparamètre discret est modélisé à l'aide de hp.choice dans l'espace de recherche. Hyperopt générera des valeurs continues dans cet espace, mais lors de l'évaluation réelle de la fonction objective, il convertit la valeur en un entier pour utiliser la valeur discrète.

Les hyperparamètres discrets sont généralement transformés en variables continues pour être optimisés. Par exemple, si vous avez un hyperparamètre qui peut prendre des valeurs discrètes comme {1, 2, 3}, vous pouvez le transformer en une variable continue qui varie dans l'intervalle [1, 3]. Cette transformation permet d'appliquer les techniques d'optimisation bayésienne standard. Lors de l'optimisation, les valeurs des hyperparamètres continus transformés sont générées de manière probabiliste en utilisant la distribution probabiliste apprise par l'optimisation bayésienne. Ensuite, ces valeurs sont arrondies aux valeurs discrètes les plus proches pour l'évaluation réelle du modèle.

Quand au CMA-ES, il est principalement conçu pour l'optimisation d'hyperparamètres continus et il ne gère pas directement les hyperparamètres discrets.

Voici un exemple d'un algorithme Ridge avec choix du paramètre alpha et solver avec cma et Hyperopt:

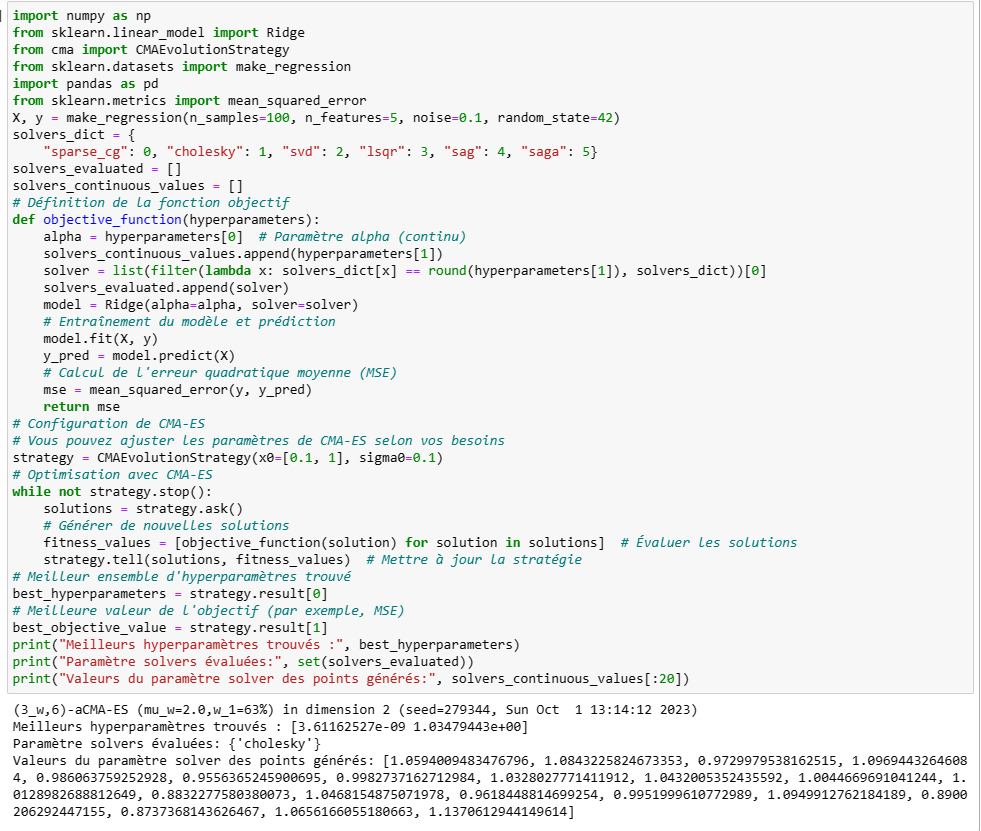
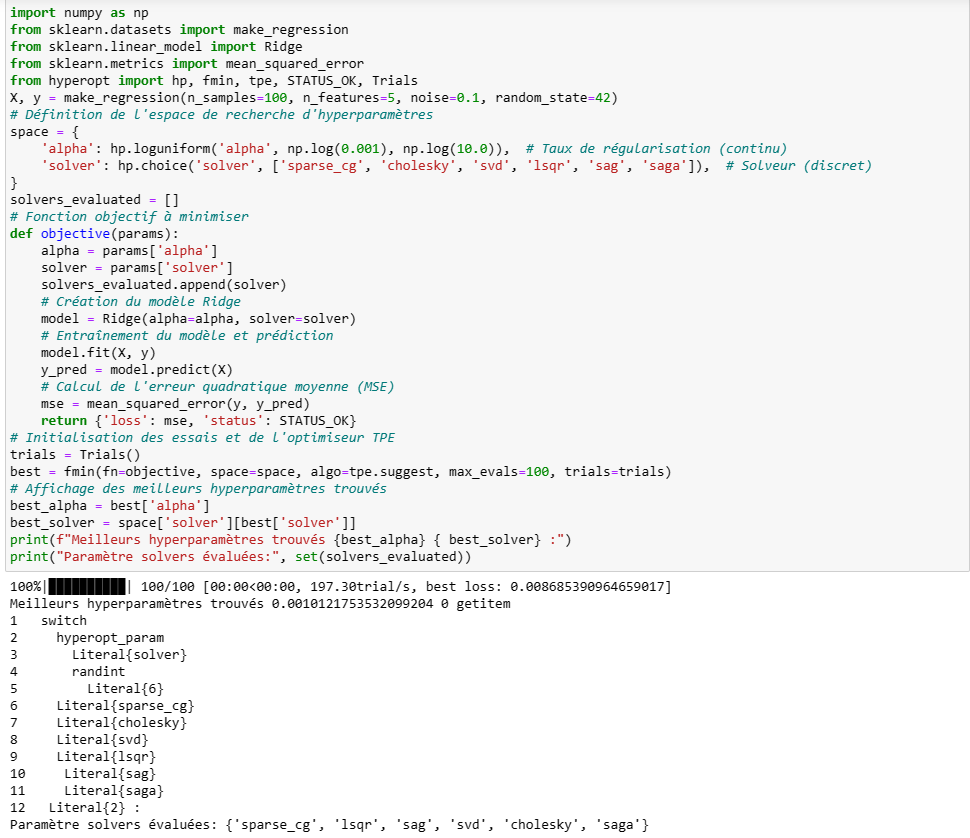
Hyperopt a évalué bien plus de valeurs du paramètre solver que cma qui  est resté sur la valeur « cholesky ». Les points générés à partir du point parent contiennent une mutation du paramètre solver, initialement à 1, qui n'est pas assez important pour changer la valeur après re-discrétisation (via la fonction round).

Il est cependant possible d'améliorer cela en ajoutant deux fonctions: une fonction qui transforme une variable discrète par une variable continue entre 0 et 1 et une fonction de rediscrétisation:

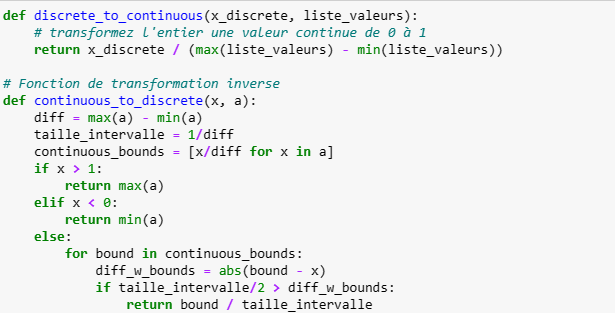
Puis modifions les lignes suivantes du code d'optimisation avec cma et réexécutons le:

On voit alors que le processus cma n'est pas cette fois ci resté bloqué sur la valeur initiale du paramètre solver car les mutations sont cette fois ci assez importantes pour changer de valeurs.

En résumé, Hyperopt gère nativement la problématique des paramètres discrets alors que l'utilisation de CMA-ES nécessite des ajustements pour permettre une meilleure gestion de ceux ci. De plus, il n'y a pas  qu'une seule manière de transformer les variables discrètes en variables continues. Cela dépendra de la nature des données et de la fonction objectif. Il est essentiel de considérer la signification des variables discrètes et de choisir une méthode qui conserve la structure et l'information importante du problème. Il faudra peut être expérimenter différentes approches pour déterminer laquelle fonctionne le mieux pour votre cas d'utilisation.

Robustesse

La robustesse est particulièrement importante dans le domaine de l'optimisation des hyperparamètres en apprentissage automatique, où les conditions peuvent varier considérablement entre les ensembles de données et les tâches. Des algorithmes robustes peuvent aider à obtenir des modèles de haute qualité sur une variété de problèmes tout en minimisant les erreurs potentielles. Pour évaluer la robustesse d'un algorithme, il est courant de le tester dans une variété de scénarios et de conditions pour voir comment il se comporte face à des perturbations ou des variations.

Ici nous allons effectuer un test simple: tester l'efficacité et la convergence des algorithmes CMA-ES et hyperopt en fonction des valeurs prises par un de leur paramètre.

Le graphique ci dessous représente la convergence du cma (valeur de la fonction de rosenbrock en fonction des itérations)  pour 4 valeurs de l'attribut popsize (nombre de solutions candidates à évaluer à chaque génération):

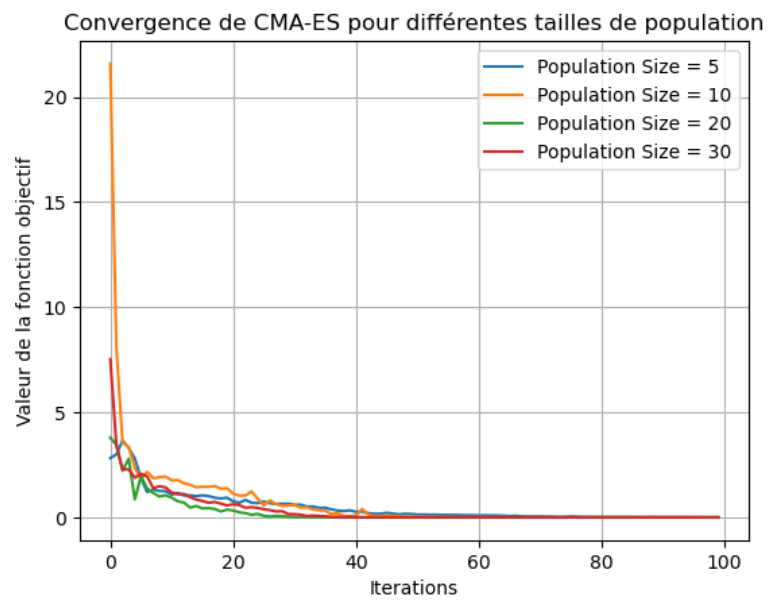
Les paramètres du cma (taille initiale de la covariance sigma, nombre de solutions enfants lambda, nombre de survivants par générations mu) vont avoir un effet sur la rapidité de la convergence car ils influencent la manière dont l'algorithme évolue dans l'espace de recherche et comment il explore et exploite les solutions. Ici, par exemple, le nombre de solutions enfants générées à chaque itération influe sur le compromis entre exploration et exploitation. Augmenter lambda encourage l'exploration en générant un plus grand nombre de solutions à évaluer.

Cela dit, hormis les différences constatées au démarrage de l'algorithme, on voit bien que les trajets sont identiques, et presque confondus à partir de 40 itérations. Le résultat, prévisible, tient au fait que le CMA-ES, comme expliqué précédemment se « dirige » vers les régions les plus prometteuses. Donc, quelques soient les conditions initiales, l'algorithme va ajuster la covariance pour retrouver la « bonne » direction.

Le graphique ci dessous montre, en revanche, que Hyperopt peut être plus sensible au choix de l'algorithme de suggestion (stratégies d'échantillonnage). Ce paramètre  peut influencer les performances d'Hyperopt:

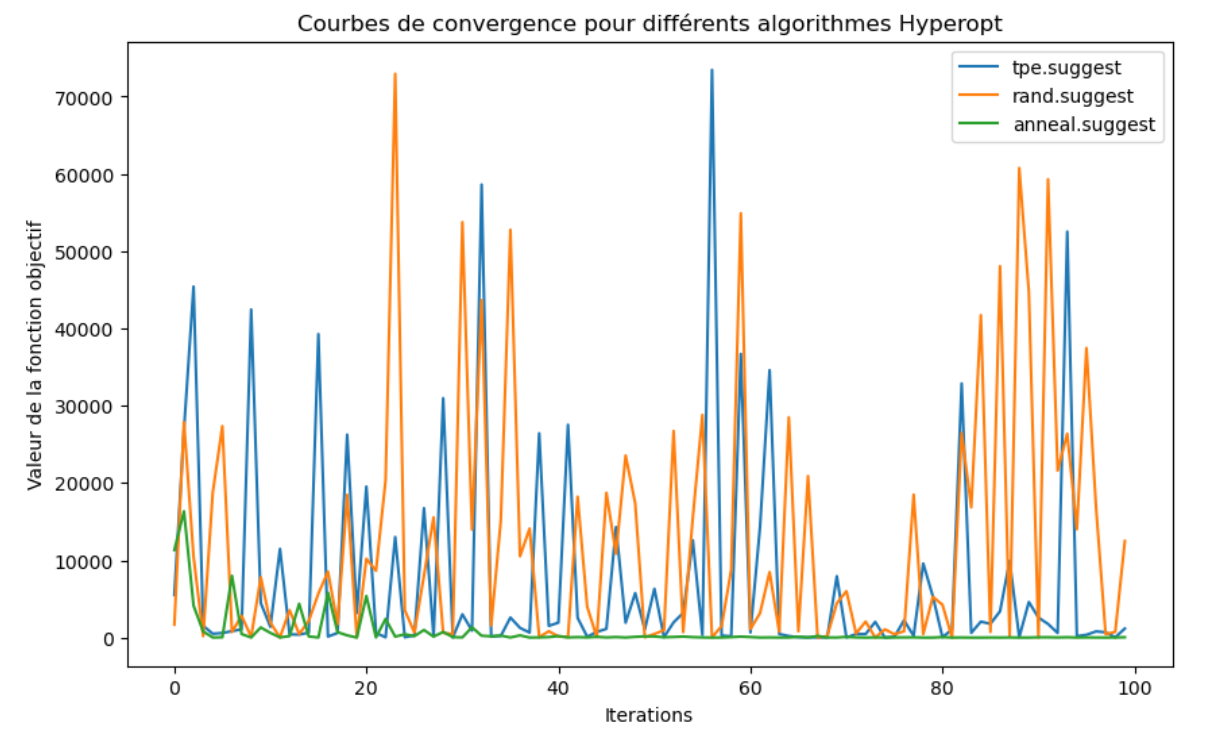
L'anneal.suggest est une méthode qui suit une stratégie similaire à celle du recuit simulé, explorant l'espace de recherche en fonction d'une température décroissante. Au fur et à mesure de la progression, la recherche devient de plus en plus locale. Cet algorithme est utile lorsque la fonction objective présente des régions mal définies, ce qui est le cas de la fonction de Rosenbrock. Cela explique pourquoi cette méthode présente la meilleure convergence sur le graphique ci dessus.

Conclusion

Bien que Hyperopt soit spécifiquement conçu pour l'optimisation des hyperparamètres dans le domaine de l'apprentissage automatique et qu'il est bien adapté pour trouver les meilleures combinaisons d'hyperparamètres pour les modèles ML, on constate que le CMA-ES, algorithme d'optimisation plus généraliste, présente bien des atouts, notamment sa rapidité de convergence et sa robustesse.

Cela dit, il est principalement conçu pour des paramètres continus et bien qu'il puisse être utilisé pour des problèmes discrets, il excelle davantage dans l'optimisation de paramètres continus. Ce dernier souci peut être résolu en gérant la transformation des variables discrets en amont mais la stratégie choisie doit être ajustée en fonction de la complexité de la fonction objectif. De plus, si la fonction objectif comporte plusieurs variables discrètes, chose assez courante en ML, la gestion de ces variables peut nécessiter une stratégie différente par variable.

En résumé, le choix entre Hyperopt et CMA-ES dépendra du domaine d'application, du type de paramètres, de la complexité de l'espace de recherche et de la présence de bruit dans les évaluations de la fonction objectif. Il est également possible d'explorer des combinaisons d'algorithmes pour tirer parti des avantages de chacun.