Le choix des hyperparamètres est un aspect critique de la construction de modèles de machine learning performants. Des hyperparamètres mal choisis peuvent conduire à des modèles sous-optimaux, qui généralisent mal sur de nouvelles données. Pour sélectionner les hyperparamètres les plus appropriés, diverses approches sont disponibles, dont certaines des plus courantes sont GridSearchCV et RandomizedSearchCV. Bien que ces méthodes soient utiles et faciles à mettre en œuvre, elles peuvent présenter des limites lorsqu’il s’agit d’explorer de vastes espaces de recherche ou d’optimiser des modèles complexes.

Illustrons cela en comparant les méthodes GridSearchCV, RandomizedSearchCV et Hyperopt sur une régression Ridge effectuée sur l’ensemble de données connu sous le nom de « Boston Housing Dataset » (bibliothèque sklearn.datasets.load_boston). Le graphique ci dessous montre les différents points évalués par les différents outils de recherche d’hyperparamètres optimaux:

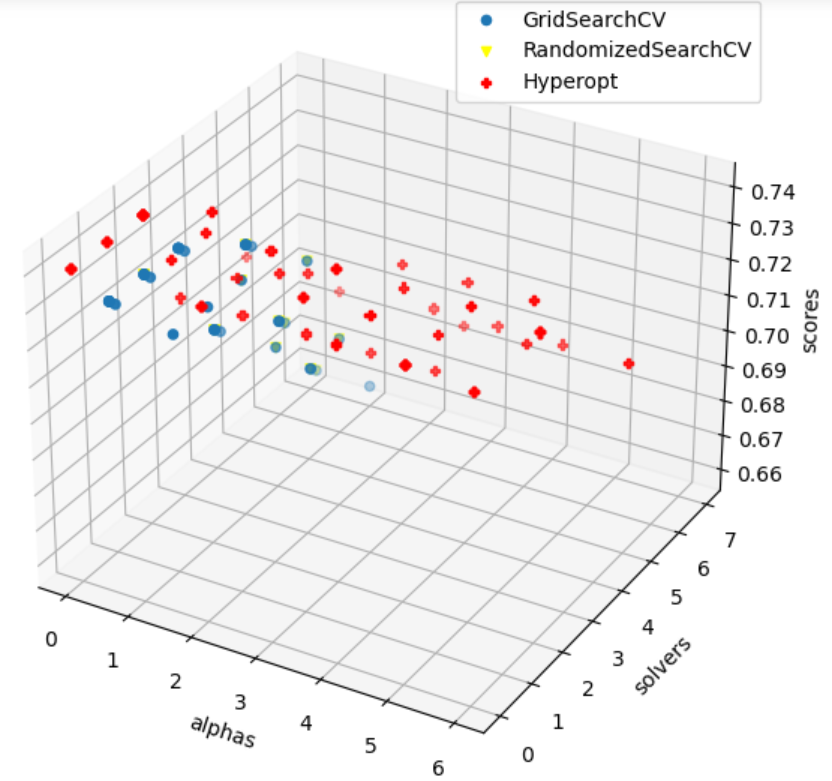
Nous remarquons que Hyperopt a trouvé une meilleure valeur d’hyperparamètre alpha et a obtenu une erreur quadratique moyenne (MSE) plus faible sur l’ensemble de test par rapport à GridSearchCV. Cela montre l’efficacité de Hyperopt pour explorer de manière plus efficace l’espace des hyperparamètres et trouver des combinaisons plus performantes pour le modèle Ridge.

L’une des principales limites de GridSearchCV est qu’il effectue une recherche exhaustive sur une grille prédéfinie d’hyperparamètres. Cela signifie que la taille de la grille détermine le nombre de combinaisons à évaluer, ce qui peut rapidement devenir prohibitif pour des problèmes avec de nombreux hyperparamètres ou des plages de valeurs continues. RandomizedSearchCV, quant à lui, effectue une recherche aléatoire à partir de distributions de valeurs prédéfinies. Bien que cette méthode puisse être plus rapide pour une exploration initiale, elle n’exploite pas efficacement les informations acquises lors des évaluations précédentes et peut ne pas converger vers les hyperparamètres optimaux.

En somme, l’utilisation de méthodes d’optimisation basées sur des algorithmes sophistiqués permet une exploration plus efficace de l’espace des hyperparamètres, ce qui réduit le temps de calcul et améliore les performances des modèles.

Optimisation bayésienne

L’optimisation bayésienne est une méthode avancée d’optimisation qui vise à trouver la meilleure configuration possible des hyperparamètres d’un modèle en utilisant des techniques probabilistes. Elle est particulièrement utile dans les domaines où les évaluations sont coûteuses en temps et en ressources, comme l’optimisation des hyperparamètres de modèles de machine learning.

Le principe de l’optimisation bayésienne repose sur l’utilisation d’un modèle probabiliste pour estimer quelle combinaison d’hyperparamètres est la plus prometteuse à explorer. L’idée est de construire et d’ajuster ce modèle en fonction des évaluations précédentes des performances du modèle avec différentes configurations d’hyperparamètres.

Il y a 3 éléments essentiels au fonctionnement de l’algorithme d’optimisation bayésienne:

• La fonction objectif: il s’agit de la fonction à optimiser. Cela peut être, par exemple, l’erreur de validation croisée, l’erreur quadratique moyenne, ou toute autre métrique que vous cherchez à optimiser.
• La fonction d’acquisition: fonction permettant de décider quelle combinaison d’hyperparamètres explorer ensuite. Il existe plusieurs techniques: expected improvement (EI), probability of improvement (PI), upper confidence bound (UCB)…
• Le modèle probabiliste (surrogate function): permet de guider de manière efficace et adaptative la recherche de la meilleure configuration d’hyperparamètres. (exemple: processus gaussien)

Pour comprendre plus précisément le rôle de ces éléments, illustrons cela en programmant une implémentation simpliste de l’optimisation bayésienne from scratch en python.

Nous essayerons d’optimiser la fonction cosinus, qui sera donc notre fonction objectif:

Puis, comme fonction d’acquisition, nous allons choisir l’EI (expected improvement). Cette méthode, à l’instar de la méthode de PI (probability of improvement) se base sur une fonction I(x) qui évalue, pour chaque x, la probabilité que le point soit mieux que le meilleur point déjà évalué:

Les f(x) étant des évaluations de la fonction objectif au point x, ils sont échantillonnées à partir d’une loi normal d’espérance et de variance  :

En posant z = (f(x) – μ(x))/σ(x), z suit une loi normale centrée réduite (d’espérance 0 et de variance 1).  On réécrit la fonction d’improvement comme suit:

PI se concentre sur la probabilité de dépasser une certaine performance seuil, tandis que EI prend en compte à la fois la probabilité et la magnitude de l’amélioration potentielle. Nous mesurons alors pour chaque point, l’espérance de l’amélioration:

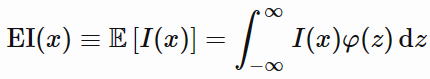
Après quelques calculs complexes, l’expected improvement s’exprime ainsi:

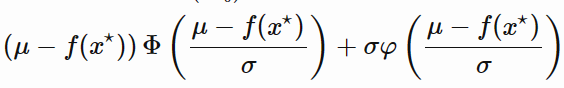
Φ étant la fonction de distribution cumulative de la loi normale centrée réduite et φ la fonction de densité de probabilité de la loi normale centrée réduite.

On peut maintenant écrire notre fonction d’acquisition:

Celle ci prend en paramètre la liste des moyennes évaluées pour chaque point, la matrice de covariance et le meilleur point évalué actuellement. Nous avons donc besoin d’un modèle probabiliste pour nous fournir les deux premiers paramètres pris par la fonction d’acquisition. Le modèle le plus utilisée est le processus gaussien. Je vous invite à consulter l’article Comprendre le processus gaussien : une approche probabiliste pour la modélisation des données si vous voulez en savoir plus sur cette méthode qui va permettre de nous fournir une approximation de la fonction objectif ainsi que l’incertitude associée.

Nous écrivons notre modèle probabiliste comme suit:

Voilà! Nous avons nos 3 méthodes, il nous suffit d’effectuer quelques itérations pour trouver le point optimum.

Définissons dans un premier temps l’intervalle sur lequel nous allons optimiser notre fonction. Nous allons rechercher l’optimum sur l’intervalle [0,5] et notre point de départ sera x=2.5 (volontairement assez loin du point optimal):

On effectue alors une dizaine d’itérations sur le processus de recherche:

Enfin, on récupère le meilleur point évalué et on trace le graphique:

On s’aperçoit alors que le maximum est retrouvé au bout de 4 itérations seulement:

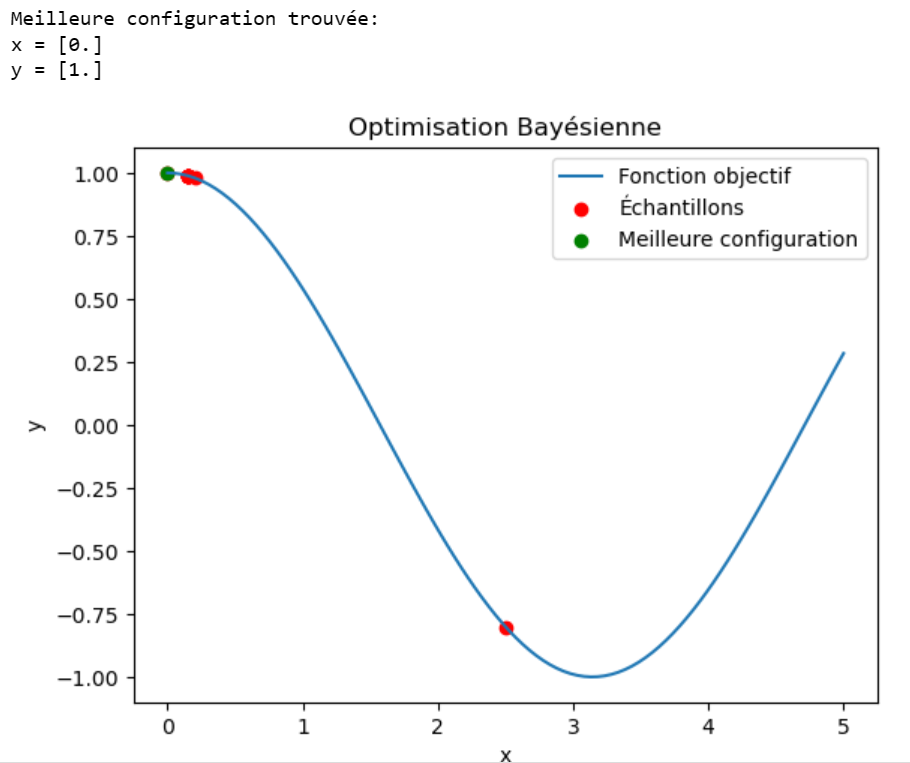
En résumé, l’optimisation bayésienne consiste à optimiser une fonction objectif en sélectionnant les meilleurs points à évaluer grâce à une fonction d’acquisition en se basant sur une évaluation de la valeur et de l’incertitude effectuée par un modèle probabiliste.

Optimisation par stratégie d’évolution

Le CMA-ES (Covariance Matrix Adaptation Evolution Strategy) est un algorithme d’optimisation évolutionnaire qui est souvent utilisé pour résoudre des problèmes d’optimisation complexes et non linéaires. L’algorithme d’optimisation par stratégie d’évolution (Evolution Strategy) est une approche basée sur la simulation de processus d’évolution biologique pour résoudre des problèmes d’optimisation.

L’idée est de générer, à partir d’un point parent et d’un paramètre de mutation, une population de candidats et de les évaluer pour ne garder que les meilleurs. Puis répéter le processus à partir des derniers points retenus.

Il existe différentes variantes d’ES dont la différence réside dans la manière dont les perturbations sont générées et utilisées pour explorer l’espace de recherche. Dans l’algorithme (1+λ)-ES (le plus simple), chaque enfant est généré en ajoutant un bruit gaussien (ou une autre perturbation) à la solution  parente. Il y a généralement une seule perturbation par enfant, d’où le nom « 1+λ » où « 1 » représente le parent et « λ » représente le nombre d’enfants.

Dans l’algorithme CMA-ES, la perturbation est générée de manière adaptative en fonction de l’expérience passée. La covariance de la distribution des solutions candidates est adaptée au fil des générations. Cela signifie que la perturbation n’est pas nécessairement une simple variation indépendante par dimension, mais plutôt une perturbation multivariée qui prend en compte les relations entre les dimensions.

L’adaptation de la covariance permet à CMA-ES de générer des perturbations qui tiennent compte de la structure du paysage de la fonction objectif, ce qui peut être très efficace pour explorer l’espace de recherche de manière adaptative.

Illustrons cela grâce à une implémentation from scratch simpliste de l’algorithme CMA-ES. Nous allons réutiliser la fonction objective utilisée pour l’implémentation de l’optimisation bayésienne.

Notre fonction cma-es prend en paramètre la fonction objective, le point initial (« ancêtre »), le nombre d’enfants par générations (population_size) et le nombre maximum de générations (et donc d’itérations avant de trouver le point optimum):

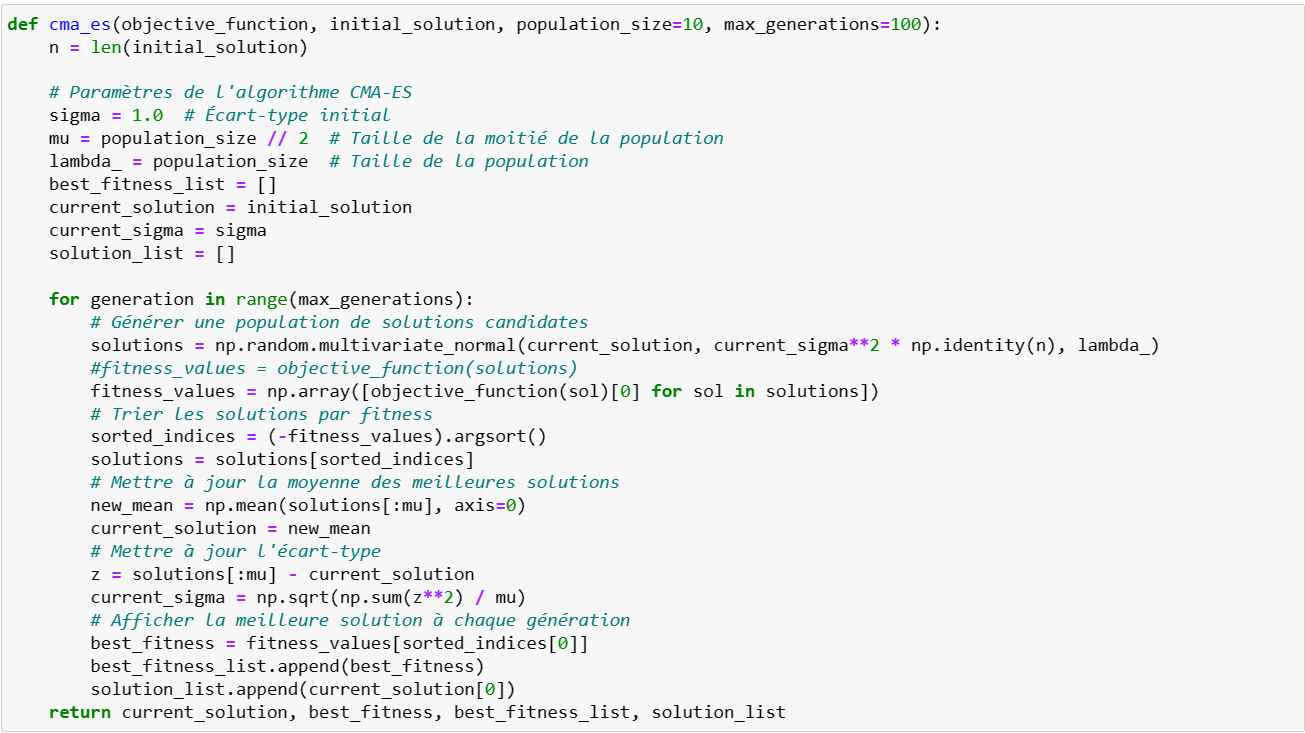
On commence par générer une génération de points enfants à l’aide d’une distribution multi normale et à partir d’une parenté (current_solution). Ces enfants sont alors évalués par la fonction objective et seules les points optimaux sont gardés.

La moyenne et la covariance sont alors mises à jour. Ici, pour des raisons pédagogiques, notre fonction ne prend qu’un seul paramètre, nous ne mettons à jour que l’écart type. Mais notez bien que l’intérêt du CMA-ES est qu’il est particulièrement efficace pour optimiser des fonctions objectives complexes dans des espaces de recherche à dimensions élevées. Il est capable de capturer les relations entre les variables d’une manière qui le distingue des méthodes d’optimisation classiques, notamment dans les espaces de recherche hautement dimensionnels.

Nous allons utiliser la nouvelle moyenne et la nouvelle variance pour générer la génération suivante et ainsi de suite.

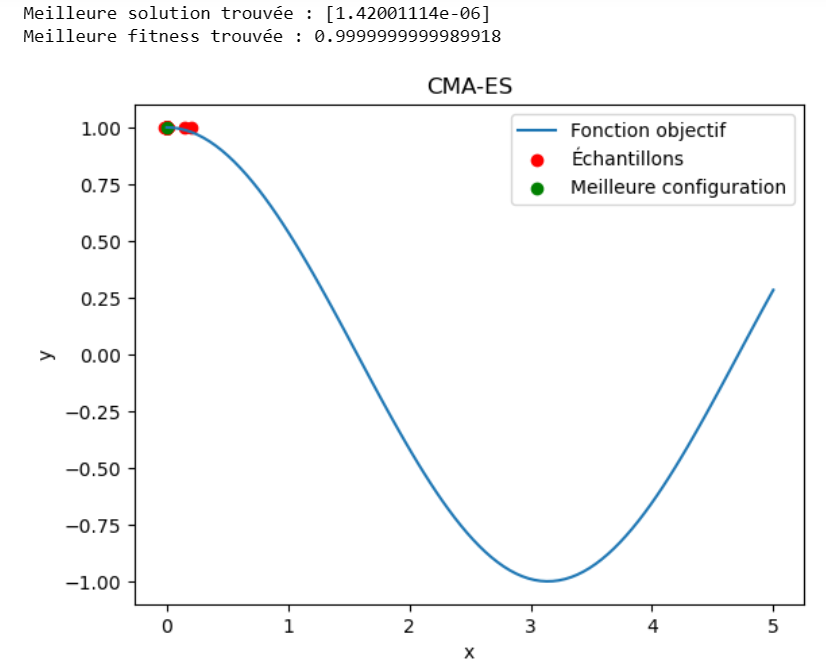
Enfin, on récupère le meilleur point évalué et on trace le graphique:

Le maximum est approché au bout de certaines itérations. Notons déjà que l’on a besoin de plus d’itérations et que cet optimum est moins précis que celui trouvé par l’optimisation bayésienne:

CONCLUSION

En résumé, l’optimisation bayésienne se concentre sur la construction d’un modèle probabiliste de la fonction objectif pour guider l’exploration, tandis que le CMA-ES se concentre sur la modélisation adaptative de la covariance des solutions candidates. Chacune de ces approches peut être plus adaptée à certains types de problèmes, en fonction de la nature de la fonction objectif et des contraintes du problème d’optimisation.

Nous allons voir en deuxième partie si le CMA-ES est adapté à la recherche des hyperparamètres en Machine Learning et dans quel cas est il une meilleure option que l’optimisation bayésienne.