Introduction

Une décision est une simplification ultime du monde. Elle concentre celui-ci en un acte « unique ». Cet acte englobe la perception que nous avons de notre environnement et des transformations potentielles de celui-ci en altérant nos objectifs immédiats sous la pression de risques collatéraux ou directement associés à cette décision.
L’informatique quantique naissante reflète cela, ceci au travers du comportement de l’unité minimum des stockage d’information, le qubit (Brassard et al., 1998) , qu’elle manipule (et qui se substitue au bit). Le qubit est perturbé au moment où un observateur le mesure. La mesure d’un qubit semble alors irréversible. Par analogie, on peut considérer la prise de décision comme l’expression d’une prise de conscience irréversible qui change le champ des possibles.
Le futur de la data science et de l’intelligence artificielle passe sans doute par une réécriture, ou tout au moins une adaptation systématique, de tous les algorithmes directement compatibles avec une représentation en manipulation de qubits (Lloyd et al., 2013). Cette réécriture ouvrira la voie pour de possibles évolutions de nos algorithmes qui leur feront profiter des propriétés intrinsèques de l’informatique quantique : la réversibilité de l’algorithme pendant son exécution, la manipulation de contextes très incertains qui peuvent se percevoir comme des univers de décision parallèles et enfin l’introduction de l’irréversibilité définitive du choix effectué lors de la prise de conscience et de l’élaboration d’une décision opérationnelle.
Pour positionner notre solution dans le futur, nous avons donc choisi de privilégier les algorithmes et les représentations du monde qui permettent la réduction de la complexité par passes successives et qui nous semble pouvoir profiter des opportunités qu’apportera la révolution informatique qui se prépare (i.e. l’informatique quantique).

Méthode

L’esprit de notre méthode

Notre méthode consiste en la réduction par passes successives de la complexité du système étudié, afin de générer des prises de décision via l’identification de signaux faibles. En anglais, nous l’avons donc nommée : « Naive complexity reduction for decision making through weak signals« . La « naïveté » de la méthode réside dans le fait que nous n’y avons introduit aucun retour arrière (back propagation), ce pour éviter de faire croître à nouveau la complexité et de prendre ainsi le risque de renoncer au point fort la démarche.

Processus d’élaboration d’une décision

La mécanique générale que nous mettons en œuvre est la suivante :

1. Choisir une représentation du monde qui se concrétise dans une certaine structuration de la donnée (les data).
2. Aborder et réduire la complexité par l’utilisation d’un ou plusieurs algorithmes en identifiant le plus soigneusement possible la nature de ce que nous avons perdu en réalisme au travers de cette réduction « éhontée » de la complexité.
3. Produire un modèle, le cas échéant « faible », ayant un ou plusieurs des objets suivants : regrouper (clustering (Luxburg, 2010)), classifier (i.e. identifier l’appartenance à une classe), fournir une régression (par exemple une tendance), déterminer un seuil, identifier un événement, identifier un signal (typiquement un signal faible et/ou avant coureur), déclencher une action, optimiser un processus d’action (typiquement en se référant aux techniques de la recherche opérationnelle – RO).

Cette mécanique est en fait parcourue plusieurs fois en parallèle et procure des modèles faibles, que l’on agrège alors dans un processus (un workflow de prise de décision), ou dans un super-modèle (l’expression consacrée en data science pour décrire un tel modèle est « model-ensemble »). Dans ses pratiques courantes, le data scientist dispose de pratiques permettant à plusieurs modèles faibles (weak model) de constituer un modèle fort, ce qui permet de compenser les faiblesses des divers modèles. Pour se convaincre de cela, il suffit d’imaginer une analogie démocratique où plusieurs personnes partagent des points de vue différents et complémentaires et votent pour converger vers une décision (agrégat de modèles faibles).
La prise de décision n’étant jamais un acte unique, le manager se trouve confronté à un faisceau de prises de décisions en fonction des actions et des réactions des autres entités avec lequel il est en concurrence, des évolutions de tendance (le marché) et enfin des conséquences directes de ses décisions précédentes. Le processus de prise de décisions successives est alors modélisable au travers de la théorie des jeux qui lui permet d’évaluer et de choisir la meilleure « gamme » de décisions. Il est commode de traiter ces enchainements de décision comme participant à un jeu par tours. Ce dernier type d’agrégation n’est pas traité dans la suite de l’article et fera l’objet de la description ultérieure d’une autre partie de nos travaux.
Le cas échéant, les différents modèles créés au travers de cette démarche peuvent à nouveau être agrégés dans un système de « poupées russes ». Il convient de noter que lorsque la complexité de l’agencement des modèles est trop importante, certaines techniques de réduction de la complexité doivent être appliquées au modèle d’agencement des modèles. En effet, on doit craindre l’instabilité et la non convergence (ou l’overfitting) d’un tel modèle de décision en « poupées russes » qui ne serait pas lui-même sous le contrôle d’une conception solide incluant la notion de complexité et de réduction de celle-ci.
Tout au long de l’élaboration d’une intelligence décisionnelle de cette nature, il faut identifier soigneusement les hypothèses qui ont présidé à nos choix d’architecture, les gains espérés, les pertes d’information et les risques embarqués par chaque décision concernant la représentation de la réalité (structure des données) et nécessitant une « certaine utilisation » d’un « certain algorithme ». La formalisation de cette attitude peut, parfois abusivement, se retrouver dans l’expression des théorèmes regroupés sous le vocable « no free lunch » (Yang, 2012).
Avant de chercher à réduire et manipuler la complexité, il faut prendre conscience de sa nature et de ses différentes formes dans le contexte de la data science.

Complexité et « machine learning »

L’apprentissage automatique par une machine, en anglais machine learning, se fonde en partie sur les probabilités et les statistiques pour inférer l’existence de classes, l’appartenance d’une observation à une classe ou la valeur d’une variable associée à une observation incomplète ou future. A la différence des systèmes experts de première génération qui encapsulaient de façon plus ou moins déterministe les règles émises par des experts humains, l’indétermination n’y pas perçue comme une difficulté périphérique gênante, mais a au contraire été intégrée au cœur de la théorie.
Edgar Morin et Jean Louis Le Moigne, dans leur ouvrage l’intelligence de la complexité (Morin et Le Moigne, 1999) nous rappellent que cette évolution est fondamentale et concomitante à l’évolution de notre pensée, y compris en physique : « … La complexité semble d’abord défier notre connaissance et, en quelque sorte, lui ordonner de régresser. Chaque fois qu’il y a irruption de la complexité sous forme d’incertitude, d’aléas, il y a une résistance très forte. Il y a eu une résistance très forte contre la physique quantique, parce que les physiciens classiques disaient : c’est le retour à la barbarie ; il n’est pas possible de nous mettre de l’indétermination alors que, depuis deux siècles, toutes les victoires de la science ont été celles du déterminisme. Il a fallu la réussite opérationnelle de la physique quantique pour que, finalement, on comprenne que la nouvelle indétermination constituait aussi un progrès dans la connaissance de la détermination elle-même. »
La réduction de la complexité dans les disciplines nombreuses branches du machine learning consiste en premier lieu dans l’encapsulation de la notion d’incertitude au sein même des abstractions qui y sont manipulées. Le cas de l’apprentissage supervisé en est une illustration directe. Celui-ci consiste globalement à élaborer un modèle (une fonction), qui permettra d’estimer les valeurs d’une variable de réponse en fonction des valeurs d’un ensemble de variables explicatives en s’appuyant sur des observations d’entrainement où l’on disposait conjointement de la valeur des variables explicatives et de la valeur des valeurs de la variable de réponse. Dans de nombreux algorithmes, le contrôle de celui-ci et sa convergence sont gérés au travers de la recherche du minimum d’une fonction de risque (i.e. mesurant des agrégats de pertes, loss en anglais), qui exprime l’erreur par rapport à la cible (Vapnick, 2006). La formalisation d’un tel algorithme peut alors sembler déterministe si l’on ne s’attache pas aux caractéristiques de la fonction de risque et à la mécanique de recherche du minimum.

Les conventions de notations suivantes permettent de poser le problème d’une façon plus rigoureuse :

• R pour Risque, X_T matrice des observations des variables explicatives,
• y vecteurs des observations des variables de réponse de l’ensemble d’entrainement,
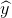•  vecteur de variable de réponse produite par le modèle (ce que l’on cherche),
• f  fonction modèle hypothèse, c’est-à-dire un modèle possible parmi plusieurs envisagés,
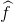•  le modèle élaboré à l’issu de l’optimisation c.a.d. une estimation de la réalité,
• T pour rappeler que l’on effectue l’optimisation sur un ensemble d’entrainement qui ne recouvre pas toute la réalité
• et enfin 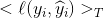 signifiant « sommation des pertes sur l’ensemble d’entrainement T ».

Le problème se formalise alors de la façon suivante :
1. Imaginons un ensemble de fonctions f, candidates à être élicitées comme étant de bons modèles de prédiction de y en fonction de X (à savoir : f(X) + aléa_tolérable = y ).
2. Posons (et donc calculons) : 
3. Puis cherchons le modèle f optimal parmi tous nos f qui minimisera : 

La complexité de la réalité est alors est masquée par le fait la fonction de risque et son traitement supportent une grande part de la technicité de l’opération qui peut se traduire par diverses interrogations :

• Existe-il un ou plusieurs minima et, en corollaire, le choix de l’algorithme d’optimisation est-il cohérent (par exemple : descente de gradient (Andrychowicz et al., 2016) versus Particule Swarm Optimization (Panigrahi et al., 2011)) ?
• Une optimisation trop efficace ne risque-t’elle pas de surdéterminer le modèle (en anglais : overfitting, la crainte des data scientists (Grus, 2015))?
• Quelle distance, quelle norme doit-on utiliser pour calculer les loss ?
• Comment les aléas de mesure de la variable de réponse du fichier d’entrainement sont-ils intégrés ?
  Ne sommes nous pas en train de minimiser les caractéristiques intrinsèques de part l’aléa de la réalité dont on cherche à apprendre, par exemple, en ne tenant pas compte de la nature bruitée de la réalité ?
• Cette façon de maîtriser la complexité stochastique ne recouvre pas l’ensemble des problèmes liés à la complexité qui nous sont posés. La complexité s’exprime et se mesure, en effet, de façons diverses.

Les systèmes réputés complexes

Les systèmes réputés complexes sont souvent constitués d’éléments (souvent appelés agents) reliés entre eux par diverses formes d’interactions. Ces interactions se visualisent dans l’espace et dans le temps. L’espace en question n’étant pas forcement notre espace physique, mais souvent un espace de représentation de ces agents en fonction de leur caractéristiques (feature space). Il existe alors un certain nombre d’indices qui laissent imaginer qu’un tel système est complexe (Mitchell, 2011) :

• quand les interactions entre agents ne sont pas linéaires,
• quand il n’existe pas de contrôle centralisé (mais il peut exister des systèmes de régulation dans des systèmes réputés complexes),
• quand les comportements émergents du système ne peuvent pas se déduire facilement (ou pas du tout) à partir de l’étude des comportements locaux ou individuels, ce qui se concrétise parfois par des structures hiérarchiques où les ensembles ne sont sémantiquement et opérationnellement pas homothétiques à chaque niveau de hiérarchie (e.g. cellule/tissus/cerveau ou individu/service/entreprise/marché),
• quand des structures hiérarchiques ou collatérales ne traitent pas l’information sous la même forme (physiquement et sémantiquement parlant),
• quand la dynamique du système est variée et non additive (c.a.d. non linéaire) par rapport aux comportements unitaires du système (fractal dans le temps, singularités …),
• quand les systèmes ont une capacité à évoluer et/ou à apprendre.

Ces indices de complexité ne sont pas exclusifs, ce qui se remarque sur les structures suivantes qui possèdent plusieurs formes de complexité :

• le cerveau,
• les villes,
• les réseaux sociaux,
• les réseaux d’agents actifs (comme les essaims, les colonies de fourmis, les agents économiques),
• les ontologies représentant la connaissance.

Pour mieux appréhender cette complexité, il nous faut donc développer des outils conceptuels variés, le plus simple d’entre eux étant la mise en place de mesures de complexité.

Mesure de la complexité et applications

Seth Llyod attire notre attention sur le fait que la variété des mesures de complexité ne reflète pas un manque d’homogénéité ou une quelconque confusion dans le champ d’étude académique de celle-ci, mais au contraire révèle notre capacité à appréhender les paramètres d’un ensemble très compact de types de complexité. Il cite notamment les types de complexités inhérentes aux caractéristiques suivantes des systèmes (Lloyd, 2017), résumées librement ici :

• les difficultés de description (exemples de mesure : entropie, information, complexité algorithmique de Kolmogorov, dimension …),
• les difficultés de création (dans notre contexte, quelques exemples utiles de mesures de la difficulté de traitement : complexité algorithmique d’un traitement, profondeur logique, profondeur thermodynamique, …),
• le degré d’organisation (exemples de mesure : complexité fractale, complexité stochastique, complexité hiérarchique, information mutuelle, complexité des arbres de décision …).

Le lecteur voulant aborder les mesures de complexité d’une façon plus formelle pourra consulter (Buhrman et De Wolf, 2002). Dans notre contexte particulier, la prise de décision, nous utilisons principalement les mesures de complexité comme suit :

1. Gérer la convergence et l’optimisation de nos algorithmes ou de nos processus : c’est la première application de la mesure de la complexité quand on veut la réduire et vérifier l’efficacité de cette réduction de complexité par étapes. On peut également mesurer la vitesse de réduction de la complexité en fonction du temps (ou de l’effort que l’on a fourni) ou chercher un optimum (minimum de l’agrégat de plusieurs mesures de complexité) puis déterminer quand ou sous quelles conditions il est possible de stopper le processus de réduction de la complexité.
2. Rechercher des signaux faibles : dans le cadre de la prise de décision et l’identification de signaux faibles, nous mesurons la complexité d’un système à intervalles réguliers. L’étude de cette série temporelle résultante et la mise en regard de celle-ci avec d’autres séries temporelles nous permet alors d’identifier des événements (évolution rapide et/ou imprévue de la complexité) ou des signaux faibles au travers de techniques de détection des signaux faibles dans des séries temporelles multivariées qui ont déjà fait l’objet d’une autre publication de l’auteur (Laude, 2016).

Résultats

Illustration du processus d’élaboration de décision en environnent complexe

Pour illustrer l’élaboration d’une décision dans un environnement complexe, nous traiterons ici de l’évolution d’un graphe de réseau social dans le temps. L’idée est d’appliquer les grandes lignes de la méthode (i.e. de façon non exhaustive, mais didactique), en se concentrant sur quelques techniques bien connues, tout en réduisant la complexité manipulée par passes successives, jusqu’à obtenir un élément permettant une prise de décision (ici un signal faible).

Les différents états d’un graphe G(V,E)(t)  qui évolue dans le temps font l’objet de deux traitements :

1. le calcul d’un ensemble de caractéristiques globales du graphe comme par exemple son diamètre et sa connexité (Diestel, 2000),
2. la clusterisation du graphe (Wale et al., 2010) au travers de l’algorithme Walktrap qui s’appuie sur une marche aléatoire et sur une mesure de similarité correspondant à la probabilité que l’on atteigne un nœud au travers d’une telle marche aléatoire à partir d’un autre nœud (Pons et Latapy, 2005).

Le premier traitement nous fournit une réduction brutale de la complexité perçue en contractant toute l’information du graphe en quelques mesures (m mesures). Le deuxième traitement relève des techniques du machine learning en apprentissage non supervisé, via l’utilisation d’une heuristique relativement sophistiquée.
Nous allons à nouveau simplifier brutalement en réduisant les informations issues de la clusterisation du graphe en ne conservant que le nombre de clusters trouvés à chaque étape.
De ces deux traitements, nous avons donc extrait une série temporelle multivariée composée de plusieurs séries temporelles : 

Les m premières séries temporelles représentent les résultats des premiers traitements et la dernière le comptage du nombre de clusters, ce qui nous donne m+1 dimensions comme illustré sur la figure 1.

Figure 1 : Evolution temporelle d’un graphe sur 3 périodes avec m+1 = 3 dimensions.

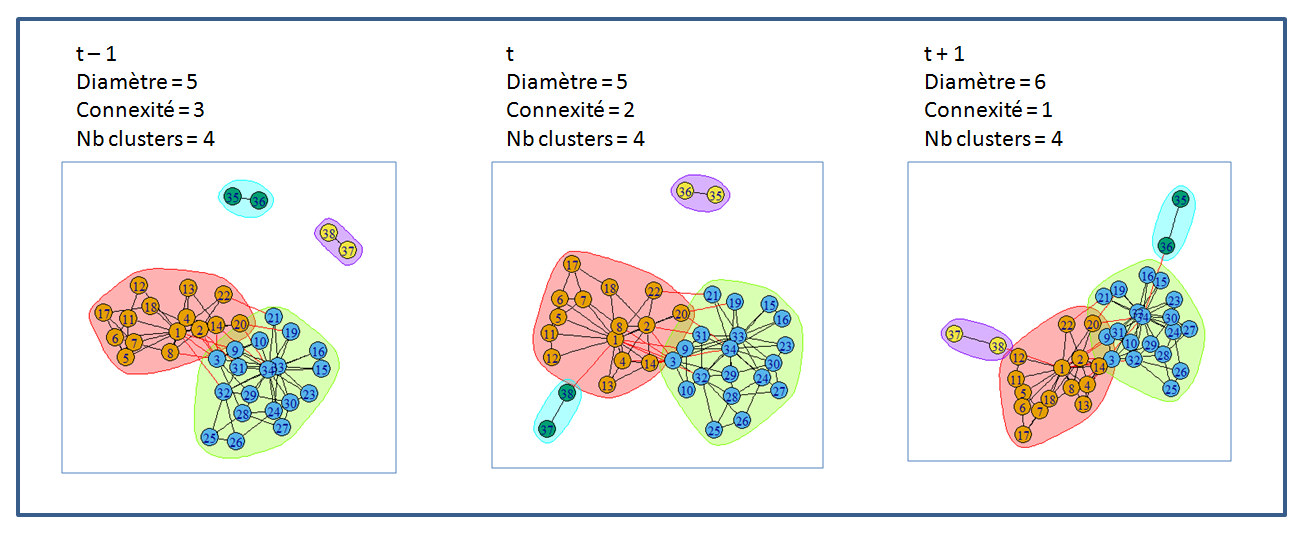
Pour diminuer drastiquement la complexité liée au m+1 dimensions du modèle, nous mesurons la dépendance mutuelle des variables sur plusieurs étapes et choisissons un petit sous-ensemble de mesures qui permettra une bonne représentation de l’ensemble. Pour ce faire, nous utilisons l’algorithme Minimum Redundancy – Maximum Relevance (De Jay et al., 2013) qui lui-même est une simplification opérationnelle du calcul de l’information mutuelle entre dimensions (features). Le calcul de l’information mutuelle aurait pu s’avérer difficile en terme de complexité algorithmique si l’on en juge par son expression mathématique, l’information mutuelle entre les m premières features et une autre feature étant :

Il était donc important d’utiliser un algorithme d’approximation de cette quantité qui soit moins complexe pour chaque feature (y variant de 1 à ) dans l’objectif d’obtenir une matrice d’information mutuelle qualitative à l’image de la figure 2.

Figure 2 : Matrice information mutuelle sous forme de « heatmap », entre 12 features

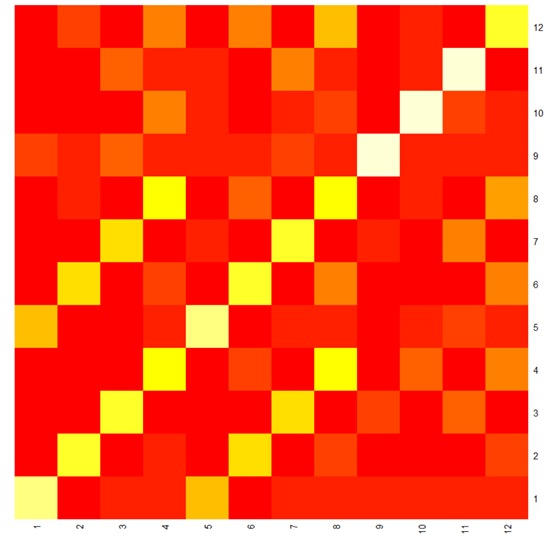
La matrice d’information mutuelle représentée ici permet de déboucher sur le choix de 3 features assez représentatives (par exemple les features 2, 5 et 8). Dans un tel cas, nous appliquerons notre algorithme de recherche de signaux faibles sur la série temporelle multivariée comportant trois séries au lieu des douze séries extraites. L’ utilisation de cet algorithme « Naive Outliers Research in V-TS » représentera à nouveau une réduction de complexité (ici dimensionnelle) importante (Laude, 2016).
L’application de cet algorithme de recherche de signaux faibles, correspondant à un comportement imprévu ou exceptionnel de la co-intégration des trois séries, représentait la dernière réduction drastique de complexité. Il débouche sur la détermination d’un petit nombre de signaux et sur une décision, ce qui est la simplification « ultime » espérée.

Conclusion

La compréhension de la façon dont s’exprime la complexité dans nos pratiques de data science par rapport aux structures des systèmes que nous manipulons, permet d’établir une méthode de réduction de celle-ci. Au travers d’un processus relativement simple, il est possible d’agencer différentes techniques algorithmiques de façon à faire décroître la complexité perçue d’un système complexe jusqu’à obtenir les éléments d’une prise de décision, le cas échéant basée sur un événement exceptionnel ou un signal faible.
Notre méthode, que nous avons surnommée « Naive complexity reduction for decision making through weak signals », pour « Elaboration de décisions au travers de la réduction de la complexité afin de générer des prises de décision via l’identification de signaux faibles », est un candidat plausible pour de telles manipulations. Le succès de celle-ci dans le cadre de notre intelligence artificielle « Deus ex Machina, une IA pour l’intelligence Economique » laisse empiriquement penser que ce processus est globalement efficace puisqu’il produit des résultats notables.
Nos futurs travaux devront confirmer ces assertions en donnant une évaluation précise des courbes de réduction de complexité sur l’ensemble des mesures de complexité que nous avons évoquées. Ces travaux complémentaires permettront la mise en place de patterns structurant l’utilisation d’une méthode formelle de réduction de la complexité ayant pour objet de déboucher sur une prise de décision.
L’ensemble des techniques utilisées pourront à terme profiter de la transition probable de nos calculateurs vers des ordinateurs quantiques.