Citation
Les auteurs
Joel TANKEU
- Société GénéralePhilippe ADIABA
- TalHenTSteve ELANGA
- Société GénéraleNadia TOUATI
- Gfi World
Copyright
Déclaration d'intérêts
Financements
Aperçu
Contenu
Introduction
Dans une ère de révolution numérique de plus en plus orientée Data driven, l’intérêt du machine Learning n’est plus à démontrer. Avec un environnement professionnel en perpétuel évolution où chaque détail compte dans le processus décisionnel, les algorithmes de machine Learning peuvent permettre de dégager un avantage stratégique capable de faire la différence.
En l’occurrence, les marchés publics représentent un cas d’étude intéressant, où l’impact d’outils d’aide à la décision performant est plus que déterminant. Dans l’environnement spécifique européen où environ 90% des procédures de passations de marchés publics sont ouvertes, cela élargit le champ des possibilités pour les fournisseurs et accroit la concurrence. Le processus d’appel d’offre reposant essentiellement sur un système d’enchère, Il est donc primordial pour ces fournisseurs de décider très rapidement s’ils doivent se positionner ou non sur un appel d’offre. Et si oui de faire la proposition juste de devis qui assurera l’équilibre parfait entre la rentabilité du marché et la satisfaction du donneur d’ordre. Dès lors, il est aisé de comprendre la mine d’or que représenterait pour un manager la capacité de prédire le nombre de candidatures qu’il y aura à un appel d’offre, ou alors le montant du marché qui sera attribué. Découvrir cette mine d’or est le défi gargantuesque auquel nous nous attaquons tout au long de cette analyse.
Données brutes
Le jeu de données utilisé pour cette étude est issu de la commande publique de l’Union Européenne et publié au Tenders Electronic Daily (TED). Les données décrivent des marchés publics de l’espace économique européen, la Suisse et l’ancienne République Yougoslave de Macédoine pour une période allant de 2009 à 2016.
Le jeu d’entraînement compte plus de deux millions de lignes et le jeu de test environ un million. Chaque instance comporte 18 variables qui définissent des informations sur les contrats (type de contrat, secteur d’activité, etc…), les attributions de marché (la procédure d’attribution, les critères d’attribution, etc…) et le type d’organisme public qui commande le marché. Les éléments à prédire sont le nombre d’offres reçues (NUMBER_OFFERS) et la valeur totale du marché sans TVA en euro (AWARD_VALUE_EUR).
Le jeu de données est constitué de 13 variables catégorielles et 5 valeurs numériques, et on note 4996 lignes dupliquées. 13 variables présentent des valeurs manquantes notamment « B_DYN_PURCH_SYST » et « B_CONTRACTOR_SME » avec respectivement 86.44 % et 85.53 % de valeurs manquantes.
Préparation des données
Après une analyse préliminaire du jeu de données, nous avons pu remarquer que le jeu de données comportait de nombreuses impuretés. D’abord en termes de valeurs manquantes ou mal renseignées, mais également du fait des lignes dupliquées. Ces dernières sont pour la plupart dues au fait que certains marchés sont subdivisés en sous-appels d’offres qui ont par conséquent les mêmes caractéristiques mais avec une valeur de marché ou un nombre de candidatures en sortie différentes. Il est pour le moment impossible de se prononcer sur l’indépendance et la pertinence de l’ensemble des variables.
Nous avons donc effectué un travail considérable de nettoyage de la donnée, à travers un ensemble d’opérations consignées dans un pipeline.
Suppression des variables inexploitables
Nous avons tout d’abord exploré pour l’ensemble des variables la distribution des valeurs possibles. L’objectif ici était de détecter s’il est possible d’appliquer des transformations sur ces valeurs afin de simplifier le modèle. Cette démarche nous a conduit à porter particulièrement notre attention sur la colonne « MAIN_ACTIVITY » qui possède 449 valeurs uniques. Un affichage des valeurs de cette colonne nous a permis de constater que chaque ligne de cette colonne était une énumération des différents secteurs d’activités gouvernementaux concernés par le marché (COFOG), chaque valeur étant séparée par une virgule (value1, value2, …, value n). Dans un premier temps nous avons opté pour transformer cette énumération, en tableau de valeurs en se basant sur le séparateur «, », mais il s’est avéré que la donnée n’était pas correctement renseignée, notamment des virgules mal positionnées dans plusieurs énumérations. Ce qui faussait la séparation des valeurs. (Par exemple, au lieu de « value1, value2 » on trouvait des cas sous la forme « va,lue1value2 »). Face à ce constat qui aurait entraîné la prise en compte de valeurs aberrantes, nous avons finalement décidé de ne pas prendre en compte la colonne « MAIN_ACTIVITY » dans l’élaboration du modèle.
En ce qui concerne les colonnes dupliquées, nous avons tout simplement décidé de supprimer les doublons et de ne garder que la première occurrence.
Analyse de l’indépendance des variables
En prenant pour acquis que les variables numériques sont indépendantes de toutes les autres, nous avons réalisé un test de cramer sur l’ensemble des variables catégorielles (Agresti, 2017). Ce test permet de mesurer l’intensité d’une relation entre deux variables.
Ainsi pour deux variables catégorielles v1 et v2, si on note N la taille de l’échantillon, dLL le degré de liberté du tableau et le score de chi2 entre v1 et v2 sous hypothèse d’indépendance, le score de cramer v est défini par la formule suivante : v=√(x^2/(N*mindLL ))
En sociologie, v1 et v2 sont faiblement corrélées si v <0.2, moyennement corrélées si 0.2<v<0.3 et sinon, v1 et v2 sont fortement corrélées. Ainsi, le test de cramer nous permet non seulement de savoir si deux grandeurs sont liées, mais aussi de mesurer l’intensité de cette relation.
La figure ci-dessous donne la matrice du test de cramer appliquée aux variables catégorielles en entrée :
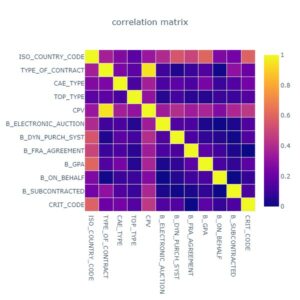
Figure 1 – Matrice de cramer des variables catégorielles
L’interprétation de cette matrice nous montre que les variables « CPV » et « TYPE_OF_CONTRACT » sont fortement corrélées (score de cramer= 0.95>0.3). Il est donc préférable de ne prendre en compte qu’une des deux. Dans une optique de réduction de la complexité du modèle, nous avons décidé de garder la colonne « TYPE_OF_CONTRACT » car elle ne possède que 9 valeurs uniques, et de mettre à l’écart la colonne « CPV » qui en possède 7690.
D’autre part, nous observons également que la variable « ISO_COUNRTRY_CODE » (représentant le pays dans lequel l’appel d’offre a été émis) est fortement corrélée à l’ensemble des variables catégorielles (tous les scores de la ligne correspondante sont supérieurs à 0.3). Cela traduit selon nous le fait que la réglementation propre à chaque pays influence la valeur de chaque variable. De ce fait, nous avons décidé de ne pas prendre en compte le code iso du pays, car l’information apportée par cette variable se retrouve implicitement définie dans toutes les autres variables.
Traitement des valeurs manquantes
Le jeu de données d’entraînement laissait apparaître des valeurs manquantes aussi bien dans les variables en entrée que dans les variables cibles.
Ainsi pour les variables cibles, nous avons fait le choix de supprimer toutes les lignes du jeu de données où une observation est non renseignée. Pour chaque variable à prédire, nous avons donc généré un jeu de données en s’assurant de ne garder que les valeurs non nulles. Le nouveau jeu de données pour prédire le nombre de candidatures à un appel d’offre représente donc 85% du fichier initial (environ 1,9 Millions de lignes) tandis que le second pour prédire la valeur du marché est identique au jeu de données initial car aucune valeur nulle n’a été recensée pour cette variable cible.
Pour les valeurs manquantes dans les variables en entrée, nous avons décidé de les remplacer en suivant la stratégie définie par le tableau ci-dessous :
| Colonne | Valeur remplaçant les valeurs nulles | Explication |
| LOTS_NUMBER | Valeur moyenne de la colonne | Variable numérique |
| CRIT_PRICE_WEIGHT | Valeur moyenne de la colonne | Variable numérique |
| NUMBER_AWARDS | Valeur moyenne de la colonne | Variable numérique |
| TYPE_OF_CONTRACT | undefined | |
| CAE_TYPE | undefined | |
| TOP_TYPE | undefined | |
| B_ELECTRONIC_AUCTION | OPE | OPE est le mode de la colonne : fréquence de 90% |
| B_DYN_PURCH_SYST | N | N est la valeur la plus fréquente |
| B_FRA_AGREEMENT | undefined | |
| B_GPA | undefined | |
| B_ON_BEHALF | Undefined | |
| B_SUBCONTRACTED | undefined | |
| CRIT_CODE | Undefined |
Encodage des variables catégorielles : One hot encoding
Les algorithmes d’apprentissages statistiques ne traitent en entrée que des valeurs numériques. Or notre jeu de données étant en grande majorité constitué de variables catégorielles, il était donc nécessaire pour nous de procéder à une transformation de ces variables afin de pouvoir les exploiter. Pour ce faire, nous avons opté pour la méthode du one hot encoding car elle permet un encodage simple des valeurs catégorielles sans biaiser l’information de la donnée par une relation d’ordinalité inexistante.
Le one hot encoding prend une variable catégorielle X, et génère une nouvelle variable booléenne (0 ou 1) pour chaque valeur de la catégorie sous la forme X_value (Kedar Podtar, 2017). Cette technique a cependant l’inconvénient d’augmenter le nombre de variables, ce qui peut significativement augmenter la complexité du modèle dans l’éventualité où on aurait des variables pouvant prendre un nombre conséquent de valeurs. De plus, elle rend plus complexe l’interprétabilité des résultats, car l’impact d’incidence sur la valeur à prédire n’est plus lié aux variables mais plutôt à des valeurs précises des variables.
Le one hot encoding s’implémente assez facilement en utilisant la fonction « OneHotEncoder » de la bibliothèque python sklearn.
From sklearn.preprocessing import OneHotEncoder # On importe la fonction Dataset = pd.read_excel(path) #path est le chemin relatif du fichier contenant le jeu de donnée categorical_features = [col1, col2, coln] #où col1, col2 et coln sont les noms des colonnes du dataset que l'on souhaite encoder encoder = OneHotEncoder(handle_unknown='ignore', categories=[dataset[col].unique() for col in categorical_features]) #on définit l’encodeur en fonction des paramètres souhaités Dataset_encoded = encoder.fit(dataset) #dataset_encoded est le nouveau Data frame avec les colonnes issues du OneHotEncoder
Le vecteur obtenu via le one hot encoding des variables catégorielles a ensuite été concaténé avec les valeurs normalisées (centrées et réduites sur les caractéristiques de leurs distributions respectives) des variables numériques présentes initialement dans le problème afin de constituer la base d’apprentissage de notre modèle.
Résultats de prédictions
Une fois terminé le processus de préparation des données, nous avons extrait un jeu de données différent pour chaque variable cible, avant de les scinder en jeu d’entraînement et jeu de validation dans une proportion de 90/10. Nous avons ensuite entraîné 3 modèles sur chaque jeu d’entraînement avant de mesurer le RMSE. Vu le large spectre des valeurs prises par la variable des montants de marchés (compris entre et ), le modèle s’est entraîné dans ce cas à prédire la valeur logarithmique de la colonne cible. Les scores obtenus sont consignés dans le tableau ci-dessous :
| Modèle | Train set nombre d’offres | Validation set nombre d’offres | Train set du log montant du marché | Validation set du log montant du marché |
| Random Forest | 19.814 | 22.241 | 1.57 | 1.64 |
| Decision Tree | 19.802 | 19.25 | 1.56 | 1.63 |
| Artificial neural network | 22.57 | 22.241 | 1.84 | 1.86 |
Le RMSE ou erreur quadratique moyenne, représente la racine de la moyenne arithmétique des carrés des écarts entre prévisions du modèle et observations. Donc la précision du modèle est inversement proportionnelle au RMSE. Au vu des résultats du tableau ci-dessus, nous avons donc décidé de choisir le modèle obtenu par l’algorithme Decision Tree qui a obtenu le score le score plus bas sur les jeux de données de validation.
Nous avons réalisé les courbes d’apprentissages des deux modèles d’arbre de décision sélectionnées à base des scores du tableau :
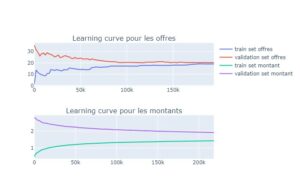
Figure 2 – Courbes d’apprentissage des modèles entraînés
Il en ressort que l’arbre de décision entraîné sur les 2 prédictions généralise bien sur les données non vues. On observe un biais faible car la valeur vers laquelle converge l’erreur du jeu d’entraînement est faible. Mais également une variance faible car c’est vers cette même valeur que converge l’erreur du jeu de validation.
Discussion
Bien que l’analyse que nous avons menée présente des résultats satisfaisants, aussi bien sur le jeu de validation que le jeu de test, il est possible d’envisager quelques perspectives d’évolution en vue d’améliorer la qualité du modèle
Tout d’abord, en ce qui concerne la variable « MAIN_ACTIVITY » que nous avons dû écarter parce qu’elle était inexploitable, la pertinence de cette donnée du fait de sa signification métier, nous fait penser que son exploitation pourrait améliorer les performances de nos modèles.
Ainsi, si nous avions eu plus de temps à disposition, nous aurions traité la donnée en procédant en 2 étapes :
- Extraire dans un tableau la dénomination complète de toutes les valeurs de la colonne. (Cette tâche est plutôt chronophage car elle nécessite un travail manuel sur le jeu de données)
- Remplacer les valeurs incomplètes ou mal tronquées par leurs valeurs correctes, en s’appuyant sur les algorithmes de calcul de distance à l’instar de Levenshtein ou fuzzywuzzy qui permettent d’établir la proximité entre les expressions. Par exemple, l’expression « Housing and co » est plus proche par calcul de distance de « Housing and community amenities » que l’expression « trolleybus or bus services ». Ainsi après comparaison de l’ensemble des distances, la valeur « Housing and community amenities » sera assigné à toute occurrence de « Housing and co »
D’autre part l’application des techniques hyperparamétrisations auraient pu significativement booster les performances du modèle.
Conclusion
En définitive nous avons mis en évidence, la possibilité de prédire avec un bon niveau de précision des indicateurs clés concernant les marchés publics, tels que le nombre de candidatures et le montant final du marché. La réussite de notre démarche réside principalement, comme dans la plupart des projets de data science, dans le soin apporté aux processus de nettoyage et préparation des données, qui sont primordiaux avant toute prédiction de machine learning.
Bibliographie
Chai, T., & Draxler, R. R. (2014). Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geoscientific model development, 7(3), 1247-1250
Levenshtein VI. Binary codes capable of correcting deletions, insertions, and reversals. Sov Phys Dokl. 1966 ; 10(8):707–10
Agresti, A. (2017). Statistical Methods for the Social Sciences. Boston
Kedar Podtar, T. S. (2017). A Comparative Study of Categorical Variable Encoding Techniques for Neural Network Classifiers. International Journal of Computer Applications.
Donath, Liliana and Milos, Marius (2008): Public sector efficiency according to COFOG classification in the European Union.
