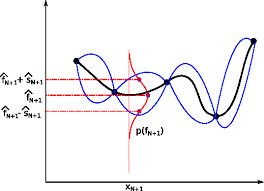
Le processus gaussien est un outil puissant utilisé dans le domaine de l'apprentissage automatique, en particulier dans le cadre de la régression et de la prédiction de séries temporelles. Il est basé sur la théorie des processus stochastiques et repose sur l'hypothèse selon laquelle les données suivent une distribution gaussienne. Dans cet article, nous explorerons les principes fondamentaux du processus gaussien, ses propriétés et son application dans divers domaines. 

Définition 

Commençons par la définition formelle d’un processus gaussien.  

Un processus gaussien est une collection de variables aléatoires, généralement infinie, où chaque combinaison finie de ces variables suit une distribution gaussienne multivariée. Un processus gaussien est entièrement défini par sa moyenne et sa covariance. 

Plus formellement encore, soit un processus gaussien défini sur un espace d'indexation X. Pour tout sous-ensemble fini d'indices Xi=x1,x2,…,xn, les variables aléatoires correspondantes  Yi=Y(x1),Y(x2),…,Y(xn) suivent une distribution gaussienne multivariée. Ainsi, le processus gaussien est caractérisé par une moyenne fonctionnelle m(x) et une fonction de covariance k(x,x′).

Cette définition peut effectivement apparaitre obscure mais ne vous inquiétez pas, cela s'éclaircira avec quelques exemples plus loin. Retenons pour le moment qu'un processus gaussien est un type spécifique de processus stochastique où chaque combinaison finie de variables aléatoires suit une distribution gaussienne multivariée. (Pour rappel, un processus stochastique est une famille de variables aléatoires pouvant suivre différentes distributions). 

Présentons tout d’abord les deux paramètres jouant un rôle crucial dans la caractérisation et la modélisation d'un processus gaussien : la moyenne et la covariance. 

Covariance et similarité 

La covariance permet de quantifier la direction et l'intensité de la relation linéaire entre les variables. Cependant, lorsqu'il s'agit de fonctions non linéaires, la covariance peut avoir des limites dans la capture de la dépendance entre les variables :  

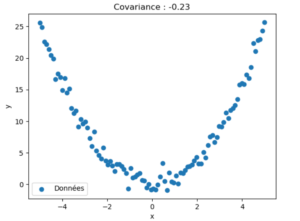
Le graphique ci-dessus représente des données non linéaires générées en utilisant la relation quadratique y = x^2 avec un bruit gaussien. Nous calculons ensuite la covariance entre les variables x et y. 

Cependant, comme la relation entre x et y est non linéaire, la covariance est limitée dans sa capacité à capturer cette dépendance. La covariance mesure principalement la tendance linéaire commune entre les variables, ce qui signifie que même si les variables sont dépendantes d'une manière non linéaire, la covariance peut être proche de zéro car elle ne tient pas compte de la relation quadratique entre les variables. 

Pour capturer les relations non linéaires entre les variables, il existe plusieurs mesures couramment utilisées : information mutuelle, corrélation de Spearman ou de Kendall, régression non linéaire etc. 

La similarité est souvent utilisée pour quantifier les relations entre les données et peut capturer des relations non linéaires. Contrairement à la covariance qui se concentre sur la dépendance linéaire entre les variables, la similarité permet d'évaluer la ressemblance ou la proximité globale des données, indépendamment de leur nature linéaire ou non linéaire. 

On appelle noyau une fonction de similarité retournant un score à partir de la distance entre deux points. Le noyau le plus utilisé est le Radial Basis Function (RBF) : 

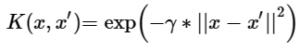
où x et x' sont deux points d'entrée, ||.|| représente une mesure de distance (par exemple, la distance euclidienne), et γ est un paramètre de contrôle qui affecte la plage d'influence du noyau. 

Cette notion de proximité dans le noyau RBF est similaire à la notion de corrélation, où des valeurs plus élevées indiquent une tendance à varier conjointement. 

Moyenne 

Dans un processus gaussien, la moyenne est considérée comme la valeur attendue de la fonction à approximer. Elle est souvent fixée à zéro pour simplifier les calculs et par convention. 

Cependant, dans certains cas, on peut estimer une moyenne non nulle en utilisant des informations a priori sur la fonction ou des connaissances préalables.  

Pour illustrer cela, générons une centaine de points d’entrée. : 

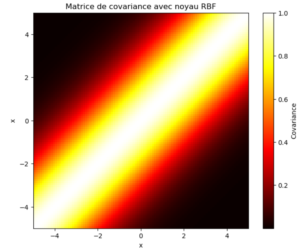
A partir de ces points, calculons la matrice de covariance à l’aide du Kernel RBF : 

Ici, nous fixons à 0.5 le paramètre l (longueur d’échelle) d’ajustement. Celui-ci contrôle la « platitude » ou la « lisibilité » du noyau RBF, ce qui affecte la façon dont la similarité décroît avec la distance entre les points. Une valeur plus faible signifie que la similarité diminue très vite avec la distance tandis qu’une valeur plus élevée signifie que la similarité décroît plus lentement avec la distance. 

Maintenant que nous avons la fonction de covariance, nous pouvons générer 5 échantillons de notre processus gaussien en fixant une moyenne de 0 : 

Nous pouvons alors calculer la moyenne des cinq échantillons pour chaque point (donc un vecteur de dimension 100) : 

Nous avons donc la moyenne et la covariance, nous pouvons donc générer un processus gaussien : 

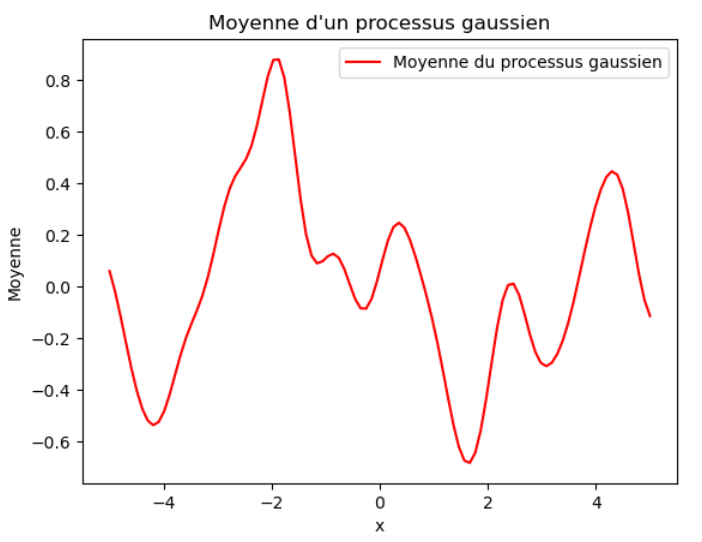
Processus gaussien et regression 

Les processus gaussiens peuvent être utilisés pour effectuer des régressions, c'est-à-dire pour estimer une fonction à partir de données observées. La régression par processus gaussien (Gaussian Process Regression en anglais) permet de modéliser la relation entre les variables d'entrée et de sortie en utilisant un processus gaussien. 

L'idée derrière la régression par processus gaussien est de considérer la fonction cible comme une réalisation d'un processus gaussien. On suppose que les observations sont des réalisations bruitées de cette fonction cible. À partir de ces observations, le processus gaussien permet d'estimer la fonction cible aux emplacements non observés en fournissant une distribution de probabilité sur les fonctions possibles.

Rappel de la loi de Bayes:  

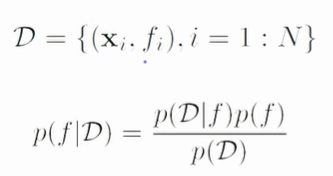
• P(f|D) est la probabilité a posteriori de la valeur de f connaissant les données. 
• P(D|f) est la probabilité d'observer les données D sachant la fonction f. 
• P(f) est la probabilité a priori de f. 
• P(D) est la probabilité d'observer les données D. 

En d'autres termes, la formule de Bayes permet de calculer la probabilité a posteriori d'un événement en combinant les informations a priori et les informations apportées par les données observées. 

Exemple: Supposons que nous ayons pour objectif d’approximer la fonction

f:x→sin(0.9x)

Calcul de la moyenne et de la covariance à priori  

Jusqu'ici nous n'avons pas de données (les f(x)). Nous avons deux à priori:

 – la moyenne  (μ_prior) est fixée à zéro car on suppose une distribution gaussienne centrée

 – les inputs similaires devraient avoir des outputs similaires. La covariance (Σ_prior) est donc calculée à l'aide d'un noyau (kernel) choisi, tel que le noyau RBF, qui capture les relations entre les points dans l'espace des données.

La formule générale pour le calcul de la covariance à priori est : Σ_prior = K(X_train, X_train), où K est la matrice de covariance basée sur le noyau appliqué aux données d'entraînement X_train: 

On utilise la décomposition de Cholesky pour calculer la racine de K (dispersion par rapport à la moyenne): 

En gros, en combinant la moyenne et la covariance à priori, le processus gaussien génère une distribution de probabilité sur les possibles f(x).

Voici les échantillons générées à partir de ces paramètres: 

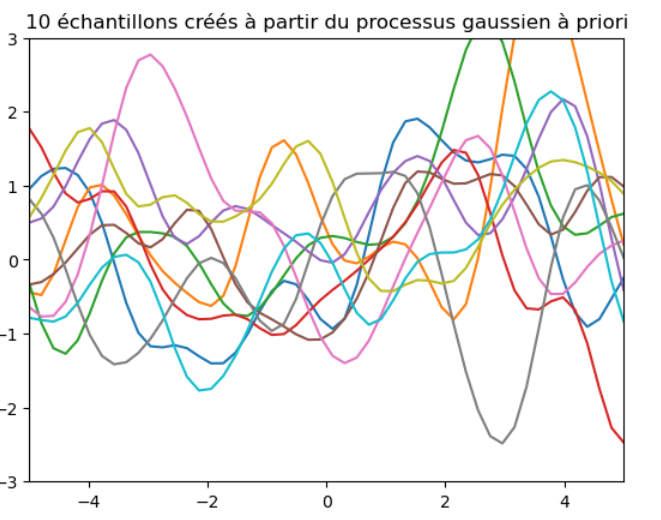
 Il est évident qu'à ce stade nous sommes très loin de notre fonction car nous n'avons intégré à notre analyse aucune information sur la fonction que nous tentons de modéliser.

Calcul de la moyenne et de la covariance à postériori  

On observe alors les valeurs pour nos données de test (ytrain) et ceux ci sont utilisées pour mettre à jour la distribution à posteriori du processus gaussien en utilisant le théorème de Bayes.

La moyenne à postériori (μpost) est calculée en utilisant les données d'entraînement et de test. Elle représente la meilleure estimation de la fonction cible à partir des données disponibles. La formule générale pour le calcul de la moyenne à postériori est :  

μpost=K(Xtest,Xtrain)∗Σprior−1∗ytrain 

où Xtest est la matrice des données de test, ytrain est le vecteur des valeurs cibles d'entraînement, et  Σprior−1 est l'inverse de la matrice de covariance à priori.   

La covariance à postériori (Σpost) représente l'incertitude associée à la prédiction de la fonction cible. La formule générale pour le calcul de la covariance à postériori est : 

Σpost=K(Xtest,Xtest)−K(Xtest,Xtrain)∗Σprior−1∗K(Xtrain,Xtest)

, où K(Xtest,Xtest) est la matrice de covariance basée sur le noyau appliqué aux données de test.   

On construit ainsi la matrice de covariance pour les données de training et de test (K(Xtrain,Xtest)):

Puis, on calcule la moyenne et la covariance du processus gaussien à postériori comme indiqué par les formules plus haut:

Traçons maintenant le graphique passant par la moyenne de nos prédictions. L'intervalle d'incertitude correspond à la moyenne plus ou moins l'écart type (la racine de la diagonale de la covariance de prédiction):

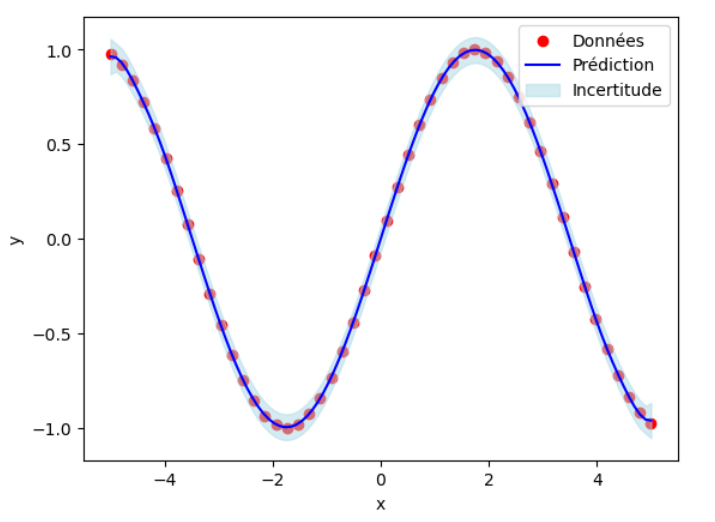
On constate bien qu’après la révision des paramètres, le processus gaussien est très proche de la fonction sin(0.9x) et l'incertitude est minime.   

Conclusion   

Les processus gaussiens permettent de modéliser des fonctions complexes en utilisant une approche probabiliste non paramétrique. Contrairement à d'autres modèles, tels que les réseaux de neurones ou les arbres de décision, les processus gaussiens offrent une flexibilité et une expressivité élevées, tout en permettant une estimation de l'incertitude associée aux prédictions.  

En utilisant un processus gaussien, nous pouvons représenter une fonction comme une distribution de probabilité sur les différentes valeurs possibles. Cette distribution est caractérisée par une moyenne et une covariance qui définissent la tendance et la variabilité de la fonction respective.  

Ils sont largement utilisés pour modéliser et analyser des séries chronologiques en raison de leur capacité à capturer les propriétés statistiques complexes de ces données (tendances, dépendances temporelles, interpolation, anomalies…).   

Dans un prochain article, nous allons effectuer un comparatif entre le processus gaussien, le modèle ARIMA et RNN pour modéliser une série chronologique.   

En attendant, n’hésitez pas à commenter cet article !