Citation
Les auteurs
Pierre Ghewy
- Université de la Polynésie française (UPF)Sébastien Chabrier
- Université de la Polynésie française (UPF)Christophe Benavent
(c.benavent@gmail.com) - Université Paris Nanterre - ORCID : https://orcid.org/0000-0002-7253-5747
Copyright
Déclaration d'intérêts
Financements
Aperçu
A l’heure où Thomas Cook vient de défaillir, les plateformes de réservation dominent le trafic de la recherche d’information. Pour être dans les premiers, la maîtrise des notes et la qualité des avis de consommateur est indispensable. Le 5 étoiles sur 5 est nécessaire. La dictature du classement impose aux hôtels de comprendre ce qui fait obtenir la meilleure note.
Contenu
Dans un premier billet nous avions identifié les principaux sujets évoqués dans le corpus des commentaires des hôtels de Polynésie. Nous avons appris que ce qui semble faire la bonne note c’est la présence dominante de deux grands thèmes axés sur la chaleur de la relation et l’intensité de l’expérience. Le but de cette seconde partie est d’approfondir cette relation et tester l’impact des sujets de commentaires sur la note donnée à l’hôtel.
La méthode va consister simplement à régresser la proportion des thèmes sur la note pour tester statistiquement leur influence.
Si l’intérêt d’une approche par topic est d’identifier les jugements de fait, ce sur quoi porte l’expérience vécue et racontée, on ne peut les défaire du jugement de valeur qui s’y associe, et c’est cet effet que l’on cherche à évaluer. Dans un même topic il peut y avoir des termes positifs, neutres ou négatifs. La proportion du discours consacré à un thème (ou sa probabilité) traduit la priorité du consommateur, ce sur quoi il focalise son attention..
En régressant ces mesures du discours sur la note on pourra ainsi évaluer la contribution des thématiques au sentiment général et disposer éventuellement d’un outil de qualification des commentaires.
Un modèle de régression ordinale
Le choix d’un modèle de régression ordinale s’impose d’emblée car il est difficile de considérer la note comme une variable continue, le peu de degrés employés (5 étoiles) conduit à la considérer comme discrète. De plus sa distribution déviée fortement à droite, laisse à penser que ce système mesure une réponse binaire (4 et surtout 5 marquent la satisfaction, les autres notes sont une désapprobation) : les intervalles entre les niveaux de l’échelle ne sont sans doute pas de même valeur.
Ces modèles ont été introduits par (McCullagh 1980) et font l’objet d’applications en sciences sociales dès le milieu des années 80 (Winship et Mare 1984) . Dans notre cas on choisira la spécification la plus classique, celle d’un modèle logit ordonné qui diffère du modèle classique par la constante qui est associée à chaque niveau de la variable ordinale. Elle partage l’idée de ratio proportionnel qui signifie que le ratio de probabilité d’avoir moins qu’une certaine note par rapport à son complémentaire (la probabilité que la note soit supérieure à ce niveau) reste constant quelques soient les variables explicatives.
Dans l’équation ci-dessus, les bêta (𝛽) sont les coefficients que l’on cherche à estimer et les c sont les constantes associées aux niveaux de l’échelle.
L’implémentation dans r est disponible au travers de plusieurs packages, nous utiliserons la librairie “ordinal” maintenue par RHB. Christensen. (Winship et Mare 1984).
Un problème de variable de composition
Cependant cette spécification est imparfaite. En effet, nos variables ont la particularité d’être des variables de proportion, leur somme est de 1, ce qui introduit une colinéarité fonctionnelle dans le modèle, même si les corrélations sont empiriquement faibles. C’est un problème qui se rencontre souvent : la composition d’un matériau en chimie, la répartition entre des classes d’âge.
Le problème a été étudié et une solution proposée par (Aitchison 1986). Pour l’essentiel le problème est que si l’on fait varier une des variables, les autres sont amenées aussi à varier de manière négative (si l’une augmente, les autres diminuent nécessairement) et donc à affecter en retour la variable dépendante dont on veut mesurer l’effet. Pour résoudre ce type de problème, Aitchinson a proposé plusieurs transformations des variables dont nous reprenons l’une d’entre elles : celle des log-ratio centrés (clr),avec la fonction clr d (pour centered log ratio) du package compositions (Gerald van den Boogaart 2005) permet de les calculer facilement. C’est ce qui est fait dans le fragment de code suivant :.
code 01 :
library(composition) #pour le calcul du clr
#On transforme la note en facteur ordonné
df$Note <- factor(df$Note, c("1", "2", "3","4","5"), ordered = TRUE)
rating<-subset(df,select=c(Note))
#on calcule les clr des variables de proportions
foo<-subset(df,select=c(Cartepostale,RapportQltePx,Dithyrambe,Paradis,Pension,ChaleurRelation,Chambre,InteractionClient))
foo<-clr(foo) #la transformation
#creation du tableau
foo<-cbind(rating,foo)
Estimation du modèle
La mise en oeuvre du modèle se fait avec la fonction clm du package ordinal et ne pose aucun problème de syntaxe. En modifiant la fonction link on peut spécifier d’autres modèles par exemple le probit.
Code 02 :
# le modèle
library(ordinal)
rego <- clm(Note ~RapportQltePx+InteractionClient+Dithyrambe+Paradis+Pension+ChaleurRelation+Chambre,link = "logit",data = foo)
```
Les résultatss’analysent comme n’importe quel modèle de régression linéaire : on obtient les estimations pour chacune des variables et les tests associés (tableau 1). Les constantes sont évaluées pour chaque changement de note. Dans notre cas le fait que les sujets soient relatifs aux aménités de la chambre ou à l’expérience de la pension de famille, ne semblent pas liés à la note donnée. Ce sont des sujets neutres.
Les autres variables sont significatives au seuil de risque de 1‰, le thème de l’interaction client et du rapport qualité prix étant liés de manière négative : parler de ces sujets c’est avoir tendance à donner une note plus basse. C’est le contraire pour les autres variables : le dithyrambe (effet woah), l’expérience du paradis et la chaleur de la relation prennent une part d’autant plus importante des commentaires que l’évaluation est bonne.
Tableau 1. Résultats de l’estimation des paramètres du modèle ordinal (logit ordonné)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
RapportQltePx -0.21651 0.07774 -2.785 0.00535 **
InteractionClient -0.80081 0.08401 -9.532 < 2e-16 ***
Dithyrambe 0.51725 0.07550 6.851 7.34e-12 ***
Paradis 0.46474 0.07859 5.913 3.36e-09 ***
Pension 0.09937 0.07693 1.292 0.19643
ChaleurRelation 0.57959 0.07758 7.471 7.95e-14 ***
Chambre -0.13228 0.07773 -1.702 0.08880 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Threshold coefficients:
Estimate Std. Error z value
1|2 -3.64279 0.09308 -39.135
2|3 -2.58077 0.06005 -42.978
3|4 -1.52469 0.04195 -36.350
4|5 -0.15318 0.03292 -4.654
On préférera, plutôt que de représenter les résultats du modèle sous la forme aride d’un tableau, utiliser ce qui semble une méthode moderne et de plus en plus populaire sous la formes d’un diagramme. Dans Cet exemple est élaboré avec ggplot. On choisit de représenter les paramètres sous la forme de leur exponent (exp(b)), avec les intervalle de confiance à 95%) afin de mieux apprécier leur effet sur les probabilités en termes de odd ratio (p/(1-p)). Une valeur inférieure à 1 contracte les probabilités, et au contraire elle les augmente quand le coefficient est supérieur à 1.
Code 03 :
#extraction des paramètres
tmp1 <- tidy(rego, conf.int = TRUE, exponentiate = TRUE)
str(tmp1)
ggplot(tmp1) + aes(x = estimate, y = term, xmin = conf.low, xmax = conf.high) +
geom_vline(xintercept = 1) + geom_errorbarh(col="grey", size=1.2) + geom_point(col="blue",size=3) +scale_x_log10()+theme_minimal()
Figure 1. Résultats du modèle logit : contribution des thèmes à la note
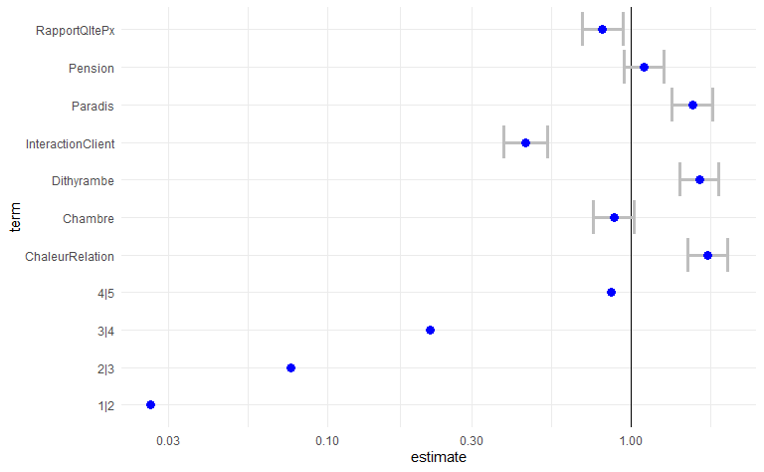
Évaluer les effets des variables avec des diagrammes d’effets
Le problème de ces modèles est qu’ils ne sont pas tout à fait des fonctions linéaires et que leur interprétation est souvent difficile. Il est difficile d’apprécier l’effet d’une variation des variables explicatives sur la variable dépendante. C’est pourquoi il est utile, sinon indispensable, de générer des diagrammes d’effets. On emploie à cette fin le package effects (Fox 2003) particulièrement bien adapté à ce type de modèle (et plus encore à la représentation des effets d’interaction que nous n’explorons pas ici mais prévu dans un autre billet).
Code 04
library(effects)
plot(predictorEffects(rego), main=list(cex=0.7,axes=list(grid=TRUE,y=list(style="stacked")),
lattice=list(key.args=list(cex=0.8, space="topleft"),layout=c(1, 1)))
Dans la figure 2, on a en abscisse le score des proportions transformées par la procédure clr pour chacun des sujets qui composent les avis, en ordonnée on a les probabilités cumulées d’avoir au moins une note donnée. Si on compare le rapport qualité prix et l’interaction client, on s’aperçoit que la probabilité d’obtenir un 5 se réduit quand la proportion de ce thème devient forte. L’effet est bien plus prononcé pour l’interaction client. Pour un score de 3 (qui correspond à une proportion presque 100%), la probabilité d’avoir une note de 5 est de moins de 10%.
Figure 2. Diagramme des effets de l’importance des sujets sur la distribution des notes
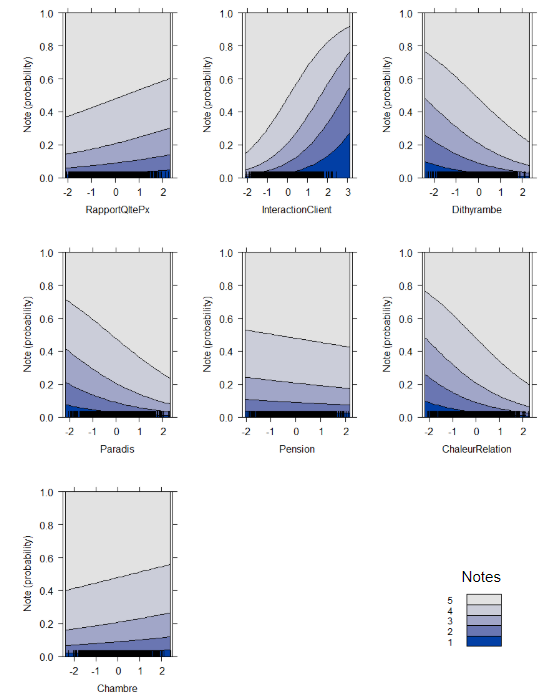
Conclusion
A l’issue de ce second billet résumons les opérations. L’objectif était de comprendre comment le contenu du texte s’associe à l’évaluation des hôtels sous la forme de note allant de 1 à 5. La méthode est une chaîne de traitements dont les étapes sont les suivantes :
- Annotation du texte tokenisé pour isoler noms communs, verbes et adjectifs
- Analyse de ce corpus par une méthode LDA pour isoler les thèmes de discussions
- Recodage des documents textuels en un vecteur de proportion des thématiques
- Transformation de ce vecteur par la méthode des centered log ratio
- Estimation d’un modèle de régression ordinale sur les notes attribuées aux hôtels
- Visualisation des résultats sous la forme de diagrammes des effets
L’ensemble permet ainsi de passer d’une analyse lexicale à une analyse purement quantifiée de la relation des contenus des documents à l’évaluation de l’objet qu’ils commentent et dont l’analyse est facilitée par la représentation graphique de modèles complexes. La tendance en effet n’est plus simplement de tester les paramètres d’un modèle ou même d’en tester la capacité prédictive à la manière du lm, mais aussi de donner de l’intelligibilité aux modèles, par souci de transparence.
Sur le fond ce que l’analyse apporte est une meilleure compréhension de la manière dont les jugements de fait et les jugement de valeurs s’associent. On retrouve ainsi cette vieille idée du mythique modèle de kano (KANO et al. 1984) : certains attributs affectent l’insatisfaction, d’autres le ravissement.
De même les discussions qui relatent une expérience (et par l’écrit la rendent littéralement mémorables) qu’elle soit celle d’une géographie (le paradis), d’un séjour somptueux (le dithyrambe) ou de la chaleur des relations nouées, portent un jugement positif pouvant aller jusqu’à 5 points sur l’échelle de notation. Quand ces thèmes sont moins présents, la note plus faible s’accompagne d’un jugement de rapport qualité-prix et des interactions avec clients.
